已知集合 A={1,2,3,4} , B={2,4,6,8} ,则 A B 中元素的个数为
A . 1 B . 2 C . 3 D . 4
B
【解析】
由题意可得 ,故
中元素的个数为 2 ,所以选 B.
【名师点睛】集合基本运算的关注点:
(1) 看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2) 有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.
(3) 注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和 Venn 图.
当 时,在同一坐标系中,函数
与
的图象是( ).
A. 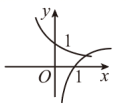 B .
B . 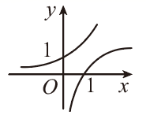
C . 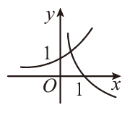 D .
D . 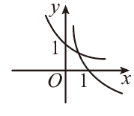
B
【分析】
根据 时指数函数
与对数函数
均为定义域内的增函数即可得答案 .
【详解】
解:因为 ,函数
为指数函数,
为对数函数,
故指数函数 与对数函数
均为定义域内的增函数,
故选: B.
已知 ,则 “
” 是 “
” 的( )
A . 充分非必要条件 B . 必要非充分条件
C . 充要条件 D . 既非充分又非必要条件
A
【分析】
“a > 1”⇒“ ” , “
”⇒“a > 1 或 a < 0” ,由此能求出结果.
【详解】
a∈R ,则 “a > 1”⇒“ ” ,
“ ”⇒“a > 1 或 a < 0” ,
∴“a > 1” 是 “ ” 的充分非必要条件.
故选 A .
【点睛】
充分、必要条件的三种判断方法.
1 .定义法:直接判断 “ 若 则
” 、 “ 若
则
” 的真假.并注意和图示相结合,例如 “
⇒
” 为真,则
是
的充分条件.
2 .等价法:利用 ⇒
与非
⇒ 非
,
⇒
与非
⇒ 非
,
⇔
与非
⇔ 非
的等价关系,对于条件或结论是否定式的命题,一般运用等价法.
3 .集合法:若 ⊆
,则
是
的充分条件或
是
的必要条件;若
=
,则
是
的充要条件.
下列函数中,在区间 上为减函数的是( )
A . B .
C .
D .
D
【分析】
根据基本初等函数的单调性及复合函数单调性求解 .
【详解】
当 时,
在
上单调递减,所以
在区间
上为增函数;
由指数函数单调性知 在区间
上单调递增;
由 在区间
上为增函数,
为增函数,可知
在区间
上为增函数;
知在区间
上为减函数 .
故选: D
若 则一定有
A . B .
C .
D .
D
【详解】
本题主要考查不等关系.已知 , 所以
,所以
,故
.故选
本卷还有45题,登录并加入会员即可免费使用哦~

该作品由: 用户乔乔分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。