2021-2022学年度高中数学导数及其应用练习题含解析
高中
整体难度：中等
2022-08-02
题号
一
二
三
四
五
评分
一、选择题 (共20题)
添加该题型下试题
1.
若 ，其中
，
，则下列结论一定成立的是（ ）
A ． B ．
C ．
D ．
难度：
知识点：导数及其应用
使用次数：277
【答案】
D
【解析】
【分析】
由题知 ，进而根据
得
，再构造函数
，结合其单调性得
，即
，进而得答案 .
【详解】
解：因为 ，其中
，
，
所以 ，其中
，
，
令 ，
，
故 时，
，
单调递减，
时，
，
单调递增，
所以 ，即
，当且仅当
时等号成立，
所以 ，
所以
故令 ，则
等价于
，
因为 ，故函数
在
单调递增，
所以 等价于
，即
所以 ，即
.
故选： D
2.
若函数 在点（ 1 ， f （ 1 ））处的切线的斜率为 1 ，则
的最小值为（ ）
A ． B ．
C ．
D ．
难度：
知识点：导数及其应用
使用次数：172
【答案】
A
【解析】
【分析】
由导数几何意义得 ，然后由基本不等式得最小值．
【详解】
由已知 ，所以
，
，当且仅当
时等号成立．
故选： A ．
3.
设函数 ，则关于
的方程
的实数根的个数不可能为（ ）
A ． 4 B ． 3 C ． 2 D ． 1
难度：
知识点：导数及其应用
使用次数：265
【答案】
A
【解析】
【分析】
利用导数确定函数 的单调性，进而得出函数
的图象，数形结合得出方程实数根的个数 .
【详解】
，
即函数 在
上单调递减，在
上单调递增
当 时，
，
，
则函数 与
的图象如下图所示
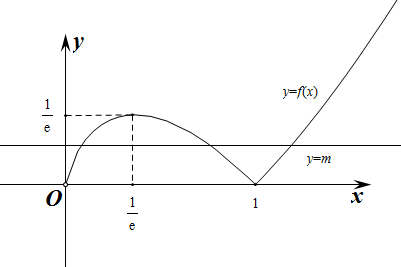
平移直线 可知，函数
与
的交点个数可能为
则关于 的方程
的实数根的个数可能为
故选： A
4.
已知函数 ，若关于
的不等式
（
是自然对数的底数）在
上恒成立，则
的取值范围是（ ）
A ． B ．
C ． D ．
难度：
知识点：导数及其应用
使用次数：111
【答案】
D
【解析】
【分析】
利用函数图像处理恒成立问题 .
【详解】
在
上恒成立，等价于
的图像恒在
直线 的上方，画出
的
图像：
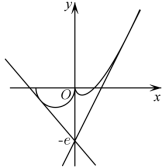
直线 恒过定点
，当直线
与 ，
相切时，设切点
，求导
得 ，可得
，由
，
解得 ，则切线的斜率为 2. 当直线
与
，
相切时，直线
与半圆
相切，由
，解得
，
由图可知， 的取值范围是
. 故 A ， B ， C 错误 .
故选： D.
5.
函数 的定义域为 R ，导函数
的图象如图所示，则函数
（ ）
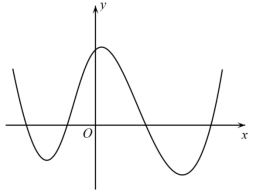
A ．无极大值点、有四个极小值点
B ．有三个极大值点、一个极小值点
C ．有两个极大值点、两个极小值点
D ．有四个极大值点、无极小值点
难度：
知识点：函数的应用
使用次数：164
【答案】
C
【解析】
【分析】
设 的图象与 x 轴的 4 个交点的横坐标从左至右依次为
，根据导函数的图象写出函数的单调区间，再根据极值点的定义即可得出答案 .
【详解】
解：设 的图象与 x 轴的 4 个交点的横坐标从左至右依次为
，
当 或
或
时，
，
当 或
时，
，
所以函数 在
，
和
上递增，
在 和
上递减，
所以函数 的极小值点为
，极大值点为
，
所以函数 有两个极大值点、两个极小值点 .
故选： C ．
本卷还有30题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
35
总体难度：
中等
难度统计
难度系数
数量
占比
中等
14
40.0%
容易
13
37.14%
偏难
3
8.57%
基础
3
8.57%
很难
2
5.71%
题型统计
大题类型
数量
占比
选择题
20
57.14%
填空题
10
28.57%
解答题
5
14.28%
知识点统计
知识点
数量
占比
导数及其应用
28
80.0%
函数的应用
2
5.71%
基本初等函数I
4
11.42%
未分类
1
2.85%
版权提示
该作品由: 用户张宁分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。