在正方体 中,
分别是
的中点,则下列说法中错误的是( )
A .
平面
B .
平面
C .
平面
D .
平面
C
【分析】连接 和
相交于点 O ,根据线面平行的判定定理可判断 ABD ,根据
可判断 C.
【详解】解:如图所示,连接 和
相交于点 O ,则 O 为
,
的中点 .

对于 A ,连接 ,则
, 因为
平面
,
平面
,
所以
平面
,故 A 正确;
对于 B ,易知
, 因为
平面
,
平面
,
所以
平面
,故 B 正确;
对于 C ,因为
, 所以
与平面
相交,故 C 错误;
对于 D ,易知
, 因为
平面
,
平面
,
所以
平面
,故 D 正确 .
故选 :C.
设 ,
是两个不同的平面,
,
是两条不同的直线,且
,
,下列结论成立的是( )
A .若 ,则
B .若
,则
C .若 ∥
,则
∥
, D .若
∥
,则
∥
A
【分析】根据线面位置关系以及面面位置关系判断 BCD ,根据面面垂直定理判断 A.
【详解】在 B 中, 与
相交,平行或异面,故 B 错;在 C 中,
与
相交或平行,故 C 错;在 D 中,
与
平行或异面,故 D 错;在 A 中,由面面垂直的判定定理,即得
,故 A 正确 .
故选: A
已知直线 在平面
内,则 “ 直线
” 是 “ 直线
” 的( )
A .充分不必要条件 B .必要不充分条件
C .充要条件 D .既不充分也不必要条件
B
【分析】根据充分条件和必要条件的定义结合线面垂直的判定和性质分析判断 .
【详解】当直线 在平面
内,
时,直线
有可能在平面
内,直线
有可能与
平行,也有可能相交不垂直,
而当直线 在平面
内,
时,
一定成立,
所以 “ 直线 ” 是 “ 直线
” 的必要不充分条件,
故选: B
在正方体 中,
是棱
上的点且
,
是棱
上的点,记
与
所成的角为
,
与底面
所成的角为
,二面角
的平面角为
,则( )
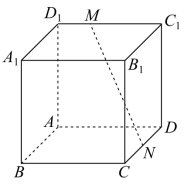
A . B .
C . D .
B
【分析】作 于
,过
作
交
于
,过
作
于
,可得
,
,
,在正方体中求得它们的正切值比较大小后可得结论.
【详解】作 于
,则
,
,从而
,
而 平面
,因此有
平面
,
过 作
交
于
,过
作
于
,则
,
,
由正方体性质易知 为二面角
的平面角,即
,
,
平面
,则
,同理
,
,
平面
,所以
平面
,
又 平面
,所以
,所以
是矩形,
,
由 平面
知
,
,
由 ,
得
,
即 ,
均为锐角,所以
,
与
重合时,三角相等.
故选: B .

一封闭的正方体容器 , P , Q , R 分别是 AB , BC 和
的中点,由于某种原因, P , Q , R 处各有一个小洞,当此容器内存水的表面恰好经过这三个小洞时,容器中水的上表面形状是( )
A .三角形 B .四边形 C .五边形 D .六边形
D
【分析】过 P , Q , R 三点的平面为六边形,可以根据平面的性质公理,先后证明其余三个顶点在 P , Q , R 所确定的平面上 .
【详解】 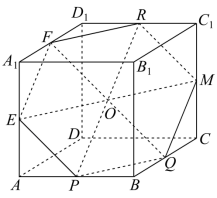
如图,设过 P , Q , R 三点的平面为平面 .
分别取 ,
,
的中点 F , E , M ,
连接 RF , FE , EP , PQ , QM , MR , EM , QF , RP .
由正方体性质知 ,所以
平面
.
又 ,所以
平面
.
又 ,所以
平面
.
所以点六边形 RFEPQM 为容器中水的上表面的形状 .
故选: D.
本卷还有30题,登录并加入会员即可免费使用哦~

该作品由: 用户心书一页分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。