2022-2023学年度高中数学——三角函数的应用练习题含解析
高中
整体难度：中等
2022-09-23
题号
一
二
三
四
五
评分
一、选择题 (共15题)
添加该题型下试题
1.
阻尼器是一种以提供阻力达到减震效果的专业工程装置．我国第一高楼上海中心大厦的阻尼器减震装置，被称为 “ 镇楼神器 ” ，如图 1 由物理学知识可知，某阻尼器的运动过程可近似为单摆运动，其离开平衡位置的位移 y (m) 和时间 t (s) 的函数关系为 ，如图 2 ，若该阻尼器在摆动过程中连续三次到达同一位置的时间分别为
，且
，
，则在一个周期内阻尼器离开平衡位置的位移大于 0.5m 的总时间为 （ ）
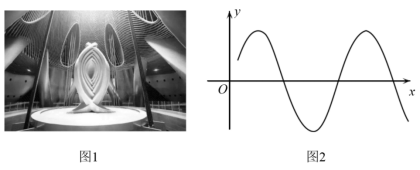
A ． B ．
C ．
D ．
难度：
知识点：三角函数
使用次数：110
【答案】
D
【分析】由条件确定函数 的周期，再由周期公式求
，再由条件关系列不等式求一个周期内阻尼器离开平衡位置的位移大于 0.5m 的总时间 .
【详解】因为 ，
，
所以 ，又
，所以
，
所以 ，
由 可得
，
所以 ，
，
，
所以在一个周期内阻尼器离开平衡位置的位移大于 0.5m 的总时间为 .
故选： D.
2.
在数学史上，为了三角计算的简便并且更加追求计算的精确性，曾经出现过下列两种三角函数：定义 为角
的正矢，记作
；定义
为角
的余矢，记作
. 给出下列结论：
① 函数 在
上单调递增；
② 若 ，则
；
③ 若 ，则
的最小值为 0 ；
④ 若 ，则
的最小值为
.
其中所有正确结论的序号为（ ）
A ． ①② B ． ③④ C ． ①③④ D ． ②③④
难度：
知识点：三角函数
使用次数：251
【答案】
D
【分析】利用定义性函数和三角函数关系式的变换判断各选项即可得到结论 .
【详解】因为 ，
所以 在
上单调递增，在
上单调递减，故 ① 错误；
因为 ，
所以
，故 ② 正确；
，
令 ，则
，
所以 ，所以
，故 ③ 正确；
因为 ，
所以 ，故 ④ 正确 .
故选： D.
3.
圭表是我国古代通过观察记录正午时影子长度的长短变化来确定季节变化的一种天文仪器，它包括一根直立的标杆（称为 “ 表 ” ）和一把呈南北方向水平固定摆放的与标杆垂直的长尺（称为 “ 圭 ” ） . 当正午阳光照射在表上时，影子会落在圭面上，圭面上影子长度最长的那一天定为冬至，影子长度最短的那一天定为夏至 . 如图是根据蚌埠市（北纬 32.92° ）的地理位置设计的圭表的示意图，已知蚌埠市冬至正午太阳高度角（即 ）约为 33.65° ，夏至正午太阳高度角（即
）约为
. 圭面上冬至线和夏至线之间的距离（即
的长）为 7 米，则表高（即
的长）约为（ ）（已知
，
）
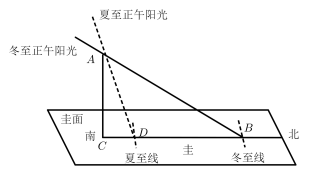
A ． 4.36 米 B ． 4.83 米 C ． 5.27 米 D ． 5.41 米
难度：
知识点：三角函数
使用次数：224
【答案】
C
【分析】由题意可求出 ，
，再由
的长为
米，求出
，即可得出答案 .
【详解】由图可知 ，
，
所以 ，
，
得 ，解得
，
故选： C.
4.
筒车是我国古代发明的一种灌溉工具， 因其经济又环保， 至今还在农业生产中得到使用 ( 图 1) ， 明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理 ( 图 2). 现有一个半径为 3 米的筒车按逆时针方向每分钟旋转 1 圈， 筒车的轴心距离水面的高度为 2 米， 设筒车上的某个盛水筒 到水面的距离为
( 单位 : 米 ) ( 在水面下则
为负数 ) ， 若以盛水筒
刚浮出水面为初始时刻， 经过
秒后， 下列命题正确的是（ ） ( 参考数据 :
)
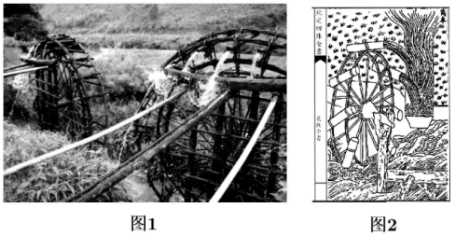
① ， 其中
， 且
，
② ， 其中
， 且
，
③ 当 时， 盛水筒
再次进入水中，
④ 当 时， 盛水筒
到达最高点 .
A ． ①③ B ． ②③ C ． ②④ D ． ①④
难度：
知识点：三角函数
使用次数：251
【答案】
C
【分析】根据题意作出示意图，如图所示，其中 为筒车的轴心的位置，
为水面，过
作
于点
，
为筒车经过
秒后的位置，连接
，过
作
于点
，首先根据已知条件求出
，进而得出
，
，即可判断 ①② ，将
代入求得的解析式可判断 ③ ，将
代入求得的解析式可判断 ④.
【详解】根据题意作出示意图，如图所示，其中 为筒车的轴心的位置，
为水面，过
作
于点
，
为筒车经过
秒后的位置，连接
，过
作
于点
，筒车的角速度为
，
由题意可知 ，
，
所以 ,
所以 ，
因为 ，
所以 ，其中
， 且
，所以 ① 错误， ② 正确，
对于 ③ ，当 时，
，
，
，所以
，故盛水筒
没有进入水中，所以 ③ 错误，
对于 ④ ，当 时，
，
，即
，所以
，所以盛水筒
到达最高点，所以 ④ 正确，
故选： C
5.
埃拉托斯特尼是古希腊亚历山大时期著名的地理学家，他最出名的工作是计算了地球（大圆）的周长 . 如图，在赛伊尼，夏至那天中午的太阳几乎正在天顶方向（这是从日光直射进该处一井内而得到证明的） . 同时在亚历山大城（该处与赛伊尼几乎在同一子午线上），其天顶方向与太阳光线的夹角测得为 . 因太阳距离地球很远，故可把太阳光线看成是平行的 . 埃拉托斯特尼从商队那里知道两个城市间的实际距离大概是 5000 斯塔蒂亚，按埃及的长度算， 1 斯塔蒂亚等于 157.5 米，则埃拉托斯特尼所测得地球的周长约为（ ）
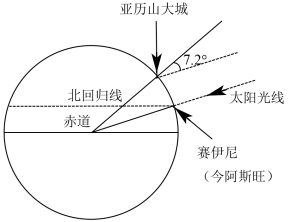
A ． 38680 千米 B ． 39375 千米 C ． 41200 千米 D ． 42192 千米
难度：
知识点：三角函数
使用次数：241
【答案】
B
【分析】由题意可将赛伊尼和亚历山大城之间的距离看作圆心角为 的扇形的弧长，由此可计算地球半径，进而求得地球周长 .
【详解】由题意可知，赛伊尼和亚历山大城之间的距离可看作圆心角为 的扇形的弧长，
设地球半径为 ，则
，
∴ 地球周长为 （米） =
（千米），
故选： B.
本卷还有30题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
35
总体难度：
中等
难度统计
难度系数
数量
占比
容易
14
40.0%
中等
17
48.57%
基础
1
2.85%
偏难
3
8.57%
题型统计
大题类型
数量
占比
选择题
15
42.85%
填空题
10
28.57%
解答题
10
28.57%
知识点统计
知识点
数量
占比
三角函数
30
85.71%
基本初等函数I
5
14.28%
版权提示
该作品由: 用户肖典军分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。