直线 与直线
相交,则实数 k 的值为( )
A . 或
B .
或
C .
或
D .
且
D
【分析】根据给定条件,利用两条直线相交的充要条件,列式求解作答 .
【详解】因直线 与直线
相交,则
,
即 ,解得
且
,
所以实数 k 的值为 且
.
故选: D
斜拉桥是桥梁建筑的一种形式,在桥梁平面上有多根拉索,所有拉索的合力方向与中央索塔一致.如下图是重庆千厮门嘉陵江大桥,共有 对永久拉索,在索塔两侧对称排列.已知拉索上端相邻两个锚的间距
均为
,拉索下端相邻两个锚的间距
均为
.最短拉索的锚
,
满足
,
,则最长拉索所在直线的斜率为( )

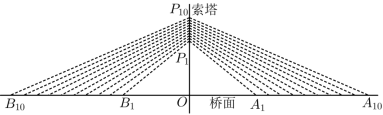
A . B .
C .
D .
C
【分析】根据题意利用已知长度可分别计算 ,
,再利用斜率的定义可解 .
【详解】根据题意,最短拉索的锚 ,
满足
,
,
且 均为
,拉索下端相邻两个锚的间距
均为
,
则 ,即点
,
同理 ,
又 ,即点
,
所以 ,
,
故选: C.
已知点 、
,若直线
与线段
相交,则实数
的取值范围是( )
A . B .
C . D .
A
【分析】求出直线 所过定点
的坐标,计算出
、
的值,数形结合可得出关于
的不等式,解之即可 .
【详解】直线 的方程化简得
,由
,可得
,
故直线 恒过定点
,故
,
,直线
的斜率为
,
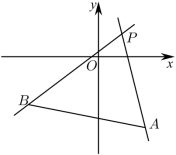
要使得直线 与线段
有公共点,则
或
,解得
.
故选: A.
已知函数 ,若满足
的整数解恰有 3 个,则实数
的范围为( )
A . B .
C .
D .
A
【分析】将问题转化为函数 的图象在直线
下方的部分有 3 个整点,然后数形结合可解 .
【详解】 得
,所以满足
的整数解恰有 3 个,等价于函数
的图象在直线
下方的部分有 3 个整点 .
如图,当直线 的斜率 m 满足
时满足题意,其中
所以, ,所以
.
故选: A
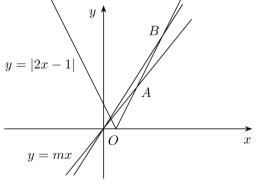
已知 是直线
的倾斜角,则 “
” 是 “
” 的( )
A .充分不必要条件 B .必要不充分条件
C .充要条件 D .既不充分又不必要条件
C
【分析】由题意可知 ,由
求出
的值,即可得出结论 .
【详解】由题意可知 ,则
,
所以, “ ” 是 “
” 的充要条件 .
故选: C.
本卷还有30题,登录并加入会员即可免费使用哦~

该作品由: 用户王瑞瑛分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。