若 ,
,求
的最小值为( )
A . B .
C .
D .
C
【分析】把 变形为
,再由基本不等式求其最小值.
【详解】 ,
,
,
当且仅当 即
时等号成立,
的最小值为
.
故选: .
已知四面体 中,
,则
体积的最大值为( )
A . B .
C .
D .
C
【分析】设 M 为 CD 的中点,连接 AM,BM , 设四面体 A - BCD 的高为 h ,利用等体积法表示出四面体的体积,利用三个正数的均值不等式即可求得答案 .
【详解】设 M 为 CD 的中点,连接 AM,BM ,
设四面体 A - BCD 的高为 h ,则 ,
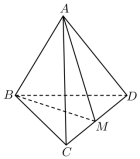
由于 ,故
,
则 , 设
,
则 ,
所以
,
当且仅当平面 ACD 与平面 BCD 垂直且 即
时取等号,
故选: C
如图,某加工厂要在一圆柱体材料中打磨出一个直三棱柱模具,已知该圆柱底面圆面积为 ,高为 6 ,则能截得直三棱柱体积最大为( )
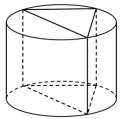
A . B .
C .
D .
B
【分析】根据直三棱柱的定义及三角形的面积公式,再利用正弦定理及三元基本不等式,结合棱柱的体积公式即可求解 .
【详解】由题意可知,设底面圆的半径为 ,则
, 解得
.
因为直三棱柱的定义可知,要使能截得直三棱柱体积最大,只需要圆的内接三角形面积最大即可,
.
当且仅当 ,即
时。等号成立,
所以三角形是正三角形时,圆的内接三角形面积最大,
.
所以能截得直三棱柱体积最大为 .
故选: B.
已知一个体积为 8 的圆柱,其底面半径为 r ,当其表面积最小时, r =( ).
A . B .
C .
D .
B
【分析】设圆柱的高为 h ,进而得到 ,再表达出表面积
,再根据三元的均值不等式求解最小值即可
【详解】设圆柱的高为 h , ∵ 圆柱的体积为 8 , ∴ ,则
,
∴ 圆柱的表面积 ,
∴ ,
当且仅当 ,即
时,等号成立
故选: B .
设 ,函数
,若
的最小值为
,则实数
的取值范围为( )
A . B .
C .
D .
A
【分析】当 时,结合不等式求得其最小值为
,当
时,
,根据函数
的最小值为
,列出不等式组,即可求解 .
【详解】当 时,
,
当且仅当 时,等号成立;
即当 时,函数
的最小值为
,
当 时,
,
要使得函数 的最小值为
,则满足
,解得
,
即实数 的取值范围是
.
故选: A.
本卷还有30题,登录并加入会员即可免费使用哦~

该作品由: 用户邵年分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。