设全集 ,集合
,则
( )
A . B .
C .
D .
A
【分析】先求出 ,再根据交集的定义可求
.
【详解】 ,故
,
故选: A.
“ 为整数 ” 是 “
为整数 ” 的( )
A .充分不必要条件 B .必要不充分条件
C .充要条件 D .既不充分也不必要条件
A
【分析】由当 为整数时,
必为整数;当
为整数时,
比一定为整数;即可选出答案 .
【详解】当 为整数时,
必为整数;
当 为整数时,
比一定为整数,
例如当 时,
.
所以 “ 为整数 ” 是 “
为整数 ” 的充分不必要条件 .
故选: A.
函数 的图像为( )
A . 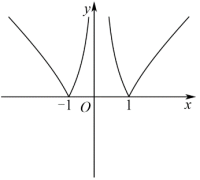 B .
B . 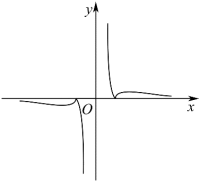
C . 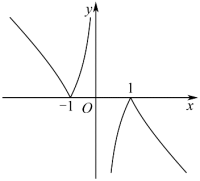 D .
D . 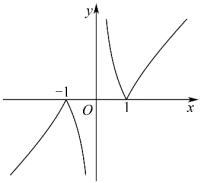
D
【分析】分析函数 的定义域、奇偶性、单调性及其在
上的函数值符号,结合排除法可得出合适的选项 .
【详解】函数 的定义域为
,
且 ,
函数 为奇函数, A 选项错误;
又当 时,
, C 选项错误;
当 时,
函数单调递增,故 B 选项错误;
故选: D.
为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位: )的分组区间为
,将其按从左到右的顺序分别编号为第一组,第二组, … ,第五组,右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有 20 人,第三组中没有疗效的有 6 人,则第三组中有疗效的人数为( )
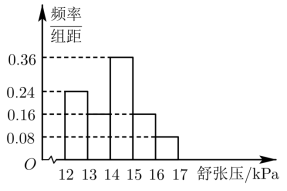
A . 8 B . 12 C . 16 D . 18
B
【分析】结合已知条件和频率分布直方图求出志愿者的总人数,进而求出第三组的总人数,从而可以求得结果 .
【详解】志愿者的总人数为 = 50 ,
所以第三组人数为 50×0.36 = 18 ,
有疗效的人数为 18 - 6 = 12 .
故选: B.
已知 ,
,
,则( )
A . B .
C .
D .
C
【分析】利用幂函数、对数函数的单调性结合中间值法可得出 、
、
的大小关系 .
【详解】因为 ,故
.
故答案为: C.
本卷还有15题,登录并加入会员即可免费使用哦~

该作品由: 用户荒村听雨分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。