《高考数学总复习系列》——高中数学必修二平面解析几何初步
高中
整体难度：中等
2012-12-07
题号
一
二
三
四
五
评分
一、解答题 (共10题)
添加该题型下试题
1.
在ΔABC中，AB=AC，∠A=900，过A引中线BD的垂线与BC交于点E，求证：∠ADB=∠CDE。
难度：
知识点：直线与方程
使用次数：108
【答案】
见图10-1，以A为原点，AC所在直线为x轴，建立直角坐标系。设点B，C坐标分别为（0,2a）,(2a,0)，则点D坐标为（a, 0）。直线BD方程为
， ①直线BC方程为x+y=2a， ②设直线BD和AE的斜率分别为k1, k2，则k1=-2。因为BD
AE，所以k1k2=-1.所以
，所以直线AE方程为
，由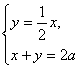
解得点E坐标为
。
所以直线DE斜率为
因为k1+k3=0.
所以∠BDC+∠EDC=1800，即∠BDA=∠EDC。
2.
设x, y满足不等式组
（1）求点(x, y)所在的平面区域；
（2）设a>-1，在（1）区域里，求函数f(x,y)=y-ax的最大值、最小值。
难度：
知识点：不等式
使用次数：167
【答案】
[解] （1）由已知得
或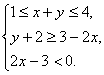
解得点(x, y)所在的平面区域如图10-4所示，其中各直线方程如图所示。AB：y=2x-5；CD：y=-2x+1；AD：x+y=1；BC：x+y=4.
(2) f(x, y)是直线l: y-ax=k在y轴上的截距，直线l与阴影相交，因为a>-1，所以它过顶点C时，f(x, y)最大，C点坐标为（-3，7），于是f(x, y)的最大值为3a+7. 如果-1<a≤2，则l通过点A（2，-1）时，f(x, y)最小，此时值为-2a-1；如果a>2，则l通过B（3，1）时，f(x, y)取最小值为-3a+1.
3.
如图10-5所示，过原点引直线交圆x2+(y-1)2=1于Q点，在该直线上取P点，使P到直线y=2的距离等于|PQ|，求P点的轨迹方程。
难度：
知识点：圆与方程
使用次数：122
【答案】
[解] 设直线OP的参数方程为
（t参数）。
代入已知圆的方程得t2-t•2sinα=0.
所以t=0或t=2sinα。所以|OQ|=2|sinα|，而|OP|=t.
所以|PQ|=|t-2sinα|，而|PM|=|2-tsinα|.
所以|t-2sinα|=|2-tsinα|. 化简得t=2或t=-2或sinα=-1.
当t=±2时，轨迹方程为x2+y2=4；当sinα=1时，轨迹方程为x=0.
4.
点A，B，C依次在直线l上，且AB=ABC，过C作l的垂线，M是这条垂线上的动点，以A为圆心，AB为半径作圆，MT1与MT2是这个圆的切线，确定ΔAT1T2垂心 的轨迹。
难度：
知识点：圆与方程
使用次数：152
【答案】
[解] 见图10-6，以A为原点，直线AB为x轴建立坐标系，H为OM与圆的交点，N为T1T2与OM的交点，记BC=1。
以A为圆心的圆方程为x2+y2=16，连结OT1，OT2。因为OT2MT2，T1HMT2，所以OT2//HT1，同理OT1//HT2，又OT1=OT2，所以OT1HT2是菱形。所以2ON=OH。
又因为OMT1T2，OT1MT1，所以
ON•OM。设点H坐标为（x,y）。
点M坐标为(5, b)，则点N坐标为
，将坐标代入
=ON•OM，再由
得
在AB上取点K，使AK=
AB，所求轨迹是以K为圆心，AK为半径的圆。
5.
已知圆x2+y2=1和直线y=2x+m相交于A，B，且OA，OB与x轴正方向所成的角是α和β，见图10-7，求证：sin(α+β)是定值。
难度：
知识点：三角函数
使用次数：102
【答案】
[证明] 过D作ODAB于D。则直线OD的倾斜角为
，因为ODAB，所以2•
,
所以
。所以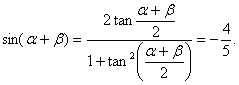
本卷还有13题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
18
总体难度：
中等
难度统计
难度系数
数量
占比
中等
13
72.22%
未分类
1
5.55%
偏难
2
11.11%
容易
2
11.11%
题型统计
大题类型
数量
占比
解答题
10
55.55%
综合题
4
22.22%
未分类
1
5.55%
选择题
3
16.66%
知识点统计
知识点
数量
占比
直线与方程
4
22.22%
数学竞赛
1
5.55%
未分类
1
5.55%
不等式
1
5.55%
圆与方程
10
55.55%
三角函数
1
5.55%
版权提示
该作品由: 用户任红玲分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。