2013数学名校试题汇编导数与应用拔高题详解.doc
高中
整体难度：偏难
2013-03-13
题号
一
二
三
四
五
评分
一、解答题 (共13题)
添加该题型下试题
2.
已知函数
.
(I)若曲线y=f(x)在点(1，f(1))处的句线与X轴平行，求函数f(x)的单调区间；
(II)若对一切正数x，都有
恒成立，求a的取值集合.
难度：
知识点：导数及其应用
使用次数：68
【答案】
（Ⅰ）∵
，
∴曲线
在点
处的切线斜率为
，
依题意
，故
，∴
，
，
当
时，
，函数
单调递增；当
时，
，函数 单调递减；所以函数的单调增区间为
，减区间为
； …6分
3.
已知函数f(x)＝lnx－mx十m,m
R.
（I）求f(x)的单调区间；
（II）若f(x)≤0。在x(0，＋00)上恒成立，求实数m的取值范围．
（III）在（II）的条件下，任意的0＜a＜b，证明：
难度：
知识点：导数及其应用
使用次数：64
【答案】
当m
0时，由（Ⅰ）得
，
令
，
，所以
，
，
，
，
，所以m=1.
综上，m的取值范围是m=1. ……………… 8分
（Ⅲ）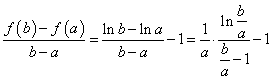
，因为
，所
以
，
由（Ⅱ）得， 
时，
，令
，则
，
又
，所以
，
因为
，所以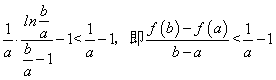
.……………… 13分
4.
若函数
对任意的实数
，
，均有
，则称函数
是区间
上的“平缓函数”.
(1) 判断
和
是不是实数集R上的“平缓函数”，并说明理由；
(2) 若数列
对所有的正整数
都有 
，设
,
求证： 
.
难度：
知识点：三角函数
使用次数：121
【答案】
当
时，同理有
成立
又当
时，不等式
，
故对任意的实数，
R,均有
.
因此 是R上的“平缓函数”. …………… 5分
由于
…………… 6分
取
，
，则
， …………… 7分
因此， 不是区间R的“平缓函数”. …………… 8分
5.
已知函数
，
=
。
(Ⅰ)求函数的最小值;
(Ⅱ)对一切
，
恒成立，求实数
的取值范围；
（Ⅲ）证明:对一切，都有
成立.
难度：
知识点：导数及其应用
使用次数：363
【答案】
本卷还有19题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
24
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
20
83.33%
偏难
4
16.66%
题型统计
大题类型
数量
占比
解答题
13
54.16%
综合题
11
45.83%
知识点统计
知识点
数量
占比
基本初等函数I
4
16.66%
导数及其应用
14
58.33%
三角函数
1
4.16%
函数的应用
3
12.5%
集合与函数的概念
1
4.16%
数学竞赛
1
4.16%
版权提示
该作品由: 用户oxofemsyk分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。