2013安徽高二下学期高中数学期中考试68356
高中
整体难度：偏难
2013-09-14
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
若复数z=3﹣i，则z在复平面内对应的点位于（ ）
|
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
难度：
知识点：数系的扩充与复数的引入
使用次数：112
【答案】
考点：
复数的代数表示法及其几何意义．
专题：
阅读型．
分析：
直接由给出的复数得到对应点的坐标，则答案可求．
解答：
解：因为复数z=3﹣i，所以其对应的点为（3，﹣1），
所以z在复平面内对应的点位于第四象限．
故选D
点评：
本题考查了复数的代数表示法及其几何意义，是基础的概念题．
2.
按流程图的程序计算，若开始输入的值为x=3，则输出的x的值是（ ）
|
| A． | 6 | B． | 21 | C． | 156 | D． | 231 |
难度：
知识点：框图
使用次数：178
【答案】
考点：
程序框图．
专题：
图表型．
分析：
根据程序可知，输入x，计算出 
的值，若≤100，然后再把 
作为x，输入 ，再计算 的值，直到 ＞100，再输出．
解答：
解：∵x=3，
∴=6，
∵6＜100，
∴当x=6时，=21＜100，
∴当x=21时，=231＞100，停止循环
则最后输出的结果是 231，
故选D．
点评：
此题考查的知识点是代数式求值，解答本题的关键就是弄清楚题图给出的计算程序．
3.
用演绎法证明函数f（x）=x3是增函数时的小前提是（ ）
|
| A． | 增函数的定义 | B． | 函数f（x）=x3满足增函数的定义 |
|
| C． | 若x1＜x2，则f（x1）＜f（x2） | D． | 若x1＜x2，则f（x1）＞f（x2） |
难度：
知识点：推理与证明
使用次数：199
【答案】
考点：
演绎推理的基本方法．
专题：
阅读型．
分析：
大前提提供了一个一般性的原理，小前提提出了一个特殊对象，两者联系，得出结论．用演绎法证明y=x3是增函数时的依据的原理是增函数的定义，小前提是一个特殊对象即函数f（x）=x3满足增函数的定义．
解答：
解：∵证明y=x3是增函数时，依据的原理就是增函数的定义，
∴用演绎法证明y=x3是增函数时的大前提是：增函数的定义，
小前提是函数f（x）=x3满足增函数的定义．
结论：函数f（x）=x3是增函数
故选B．
点评：
本题考查对三段论的理解，第一个判断称为大前提，它提供了一个一般的原理．
三段论式推理，是演绎推理的主要形式．其思维过程大致是：大前提提供了一个一般性的原理，小前提提出了一个特殊对象，两者联系，得出结论．演绎所得的结论是蕴涵于前提之中的特殊事实，结论完全蕴涵于前提之中．
4.
用火柴棒摆“金鱼”，如图所示：按照上面的规律，第n个“金鱼”图需要火柴棒的根数为（ ）
|
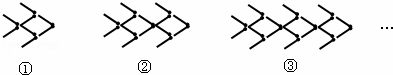
| A． | 6n﹣2 | B． | 8n﹣2 | C． | 6n+2 | D． | 8n+2 |
难度：
知识点：推理与证明
使用次数：138
【答案】
考点：
归纳推理．
专题：
规律型．
分析：
由图形间的关系可以看出，每多出一个小金鱼，则要多出6根火柴棒，则组成不同个数的图形的火柴棒的个数组成一个首项是8，公差是6的等差数列，写出通项，求出第n项的火柴根数．
解答：
解：∵第一个图中有8根火柴棒组成，
第二个图中有8+6个火柴棒组成，
第三个图中有8+2×6个火柴组成，
以此类推
组成n个系列正方形形的火柴棒的根数是8+6（n﹣1）
∴第n个图中的火柴棒有6n+2
故选C．
点评：
本题考查归纳推理，考查等差数列的通项，解题的关键是看清随着小金鱼的增加，火柴的根数的变化趋势，看出规律．
5.
计算
的结果是（ ）
|
| A． | i | B． | ﹣i | C． | 2 | D． | ﹣2 |
难度：
知识点：数系的扩充与复数的引入
使用次数：175
【答案】
考点：
复数代数形式的乘除运算．
专题：
计算题．
分析：
两个复数相除，分子和分母同时乘以分母的共轭复数，运算求得结果．
解答：
解：计算=
=
=﹣i，
故选B．
点评：
本题主要考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，属于基础题．
本卷还有14题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
19
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
17
89.47%
容易
1
5.26%
偏难
1
5.26%
题型统计
大题类型
数量
占比
选择题
10
52.63%
填空题
5
26.31%
解答题
4
21.05%
知识点统计
知识点
数量
占比
数系的扩充与复数的引入
3
15.78%
框图
1
5.26%
推理与证明
5
26.31%
集合与函数的概念
2
10.52%
导数及其应用
5
26.31%
统计
2
10.52%
算法初步
1
5.26%
版权提示
该作品由: 用户小俞分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。