2013浙江高二上学期高中数学期中考试68570
高中
整体难度：中等
2013-09-17
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（ ）
|
| A． | 若m∥α，n∥α，则m∥n | B． | 若α⊥γ，β⊥γ，则α∥β | C． | 若m∥α，m∥β，则α∥β | D． | 若m⊥α，n⊥α，则m∥n |
难度：
知识点：点 直线 平面之间的位置
使用次数：168
【答案】
解：A 不正确．因为m，n平行于同一个平面，故m，n可能相交，可能平行，也可能是异面直线．
B 不正确．因为α，β 垂直于同一个平面γ，故α，β 可能相交，可能平行．
C 不正确．因为α，β平行与同一条直线m，故α，β 可能相交，可能平行．
D正确．因为垂直于同一个平面的两条直线平行．
故选 D．
2.
已知直线m、n和平面α、β满足m⊥n，m⊥α，α⊥β，则（ ）
|
| A． | n⊥β | B． | n∥β，或n⊂β | C． | n⊥α | D． | n∥α，或n⊂α |
难度：
知识点：点 直线 平面之间的位置
使用次数：52
【答案】
解答：
解：由题意结合图形易知D正确
故选D
3.
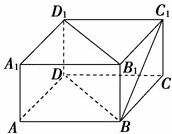
如图，在长方体ABCD﹣A1B1C1D1中，AB=BC=2，AA1=1，则BC1与平面BB1D1D所成角的正弦值为（ ）
|
| A． |
| B． |
| C． |
| D． |
|
难度：
知识点：空间几何体
使用次数：57
【答案】
解：以D点为坐标原点，以DA、DC、DD1所在的直线为x轴、y轴、z轴，建立空间直角坐标系（图略），
则A（2，0，0），B（2，2，0），C（0，2，0），C1（0，2，1）
∴
=（﹣2，0，1），
=（﹣2，2，0），且为平面BB1D1D的一个法向量．
∴cos＜，＞═
=
．
∴BC1与平面BB1D1D所成角的正弦值为
故答案为D．
4.
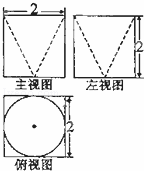
某几何体的三视图如图所示，则它的体积是（ ）
|
| A． |
| B． |
| C． | 8﹣2π | D． |
|
难度：
知识点：空间几何体
使用次数：69
【答案】
解答：
解：三视图复原的几何体是棱长为：2的正方体，除去一个倒放的圆锥，圆锥的高为：2，底面半径为：1；
所以几何体的体积是：8﹣
=
故选A．
5.
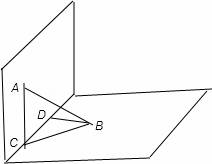
已知直二面角α﹣l﹣β，点A∈α，AC⊥l，C为垂足，点B∈β，BD⊥l，D为垂足，若AB=2，AC=BD=1，则CD=（ ）
|
| A． | 2 | B． |
| C． |
| D． | 1 |
难度：
知识点：点 直线 平面之间的位置
使用次数：167
【答案】
解答：
解：根据题意，直二面角α﹣l﹣β，点A∈α，AC⊥l，可得AC⊥面β，
则AC⊥CB，△ACB为Rt△，且AB=2，AC=1，
由勾股定理可得，BC=
；
在Rt△BCD中，BC=，BD=1，
由勾股定理可得，CD=
；
故选C．
点评：
本题考查两点间距离的计算，计算时，一般要把空间图形转化为平面图形，进而构造直角三角形，在直角三角形中，利用勾股定理计算求解．
本卷还有15题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
20
总体难度：
中等
难度统计
难度系数
数量
占比
中等
13
65.0%
容易
7
35.0%
题型统计
大题类型
数量
占比
选择题
10
50.0%
填空题
6
30.0%
解答题
3
15.0%
综合题
1
5.0%
知识点统计
知识点
数量
占比
点 直线 平面之间的位置
9
45.0%
空间几何体
9
45.0%
空间中的向量与立体几何
2
10.0%
版权提示
该作品由: 用户pynzwq分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。