2013版高中数学 11.2排列与组合课时提能训练 理 新人教B版
高中
整体难度：中等
2013-12-15
题号
一
二
三
四
五
评分
一、选择题 (共7题)
添加该题型下试题
1.
不等式
＜6×
的解集为( )
(A)[2,8] (B)[2,6] (C)(7,12) (D){8}
难度：
知识点：计数原理
使用次数：147
【答案】
D.
＜6×
，
∴x2－19x＋84＜0，又x≤8，x－2≥0，
∴7＜x≤8，x∈N＋，即x＝8.
2.
一次考试中，要求考生从试卷上的9个题目中选6个进行答题，要求至少包含前5个题目中的3个，则考生答题的不同选法的种数是
( )
(A)40 (B)74 (C)84 (D)200
难度：
知识点：计数原理
使用次数：101
【答案】
B.分三类：C
C
＋C
C
＋C
C
＝74.
3.
甲、乙、丙三名同学在课余时间负责一个计算机房的周一到周六的值班工作，每天1人值班，每人值班2天，如果甲同学不值周一的班，乙同学不值周六的班，则可以排出不同的值班表有( )
(A)36种 (B)42种 (C)50种 (D)72种
难度：
知识点：计数原理
使用次数：190
【答案】
B.每人值班2天的排法减去甲值周一或乙值周六的排法，再加上甲值周一且乙值周六的排法，共有C
C－2C
C＋CC
＝42(种).
4.
如图，三行三列的方阵中有9个数aij(i＝1,2,3；j＝1,2,3)，从中任取三个数，则至少有两个数位于同行或同列的概率是( )
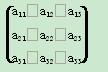(A)
(B)
(C)
(D)
难度：
知识点：计数原理
使用次数：116
【答案】
D.从9个中选3个有
种选法，要使三个数均不同行且不同列共有
种选法，所以，所求概率为1－
＝.
5.
为了迎接建国63周年国庆，某大楼安装5个彩灯，它们闪亮的顺序不固定，每个彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色，且这5个彩灯闪亮的颜色各不相同.记这5个彩灯有序地闪亮一次为一个闪烁，在每个闪烁中，每秒钟有且仅有一个彩灯闪亮，而相邻两个闪烁的时间间隔均为5秒.如果要实现所有不同的闪烁，那么需要的时间至少是( )
(A)1 205秒 (B)1 200秒 (C)1 195秒 (D)1 190秒
难度：
知识点：计数原理
使用次数：188
【答案】
C.由题知闪烁的总个数为
＝120.每次闪烁时间为5秒，知总闪烁时间为5×120＝600 s，又每两次闪烁之间的间隔为5 s，故闪烁间隔总时间为5×(120－1)＝595 s，故总时间为600＋595＝1 195 s.
本卷还有8题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
13
总体难度：
中等
难度统计
难度系数
数量
占比
容易
5
38.46%
中等
8
61.53%
题型统计
大题类型
数量
占比
选择题
7
53.84%
填空题
3
23.07%
解答题
3
23.07%
知识点统计
知识点
数量
占比
计数原理
13
100.0%
版权提示
该作品由: 用户杨政清分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。