2014高中数学期末考试76764
高中
整体难度：中等
2014-02-04
题号
一
二
三
四
五
评分
一、填空题 (共4题)
添加该题型下试题
1.
设a,b是不同的直线,α,β是不同的平面,则下列命题:
①若a⊥b,a∥α,则b∥α ②若a∥α,α⊥β,则a⊥β
③若a⊥β,α⊥β,则a∥α ④若a⊥b,a⊥α,b⊥β,则α⊥β
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
难度：
知识点：点 直线 平面之间的位置
使用次数：171
【答案】
B.①当a⊥b,a∥α时,b与α可能相交,所以①错误.②中a⊥β不一定成立.③中a⊂α或a∥α,所以错误.④正确,所以正确的有1个,所以选B.
2.
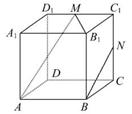如图,在正方体ABCD
-A1B1C1D1中,M,N分别是棱C1D1,C1C的中点.以下四个结论:
①直线AM与直线CC1相交;
②直线AM与直线BN平行;
③直线AM与直线DD1异面;
④直线BN与直线MB1异面.
其中正确结论的序号为 (注:把你认为正确的结论序号都填上).
难度：
知识点：点 直线 平面之间的位置
使用次数：113
【答案】
③④
【解析】由图可知AM与CC1是异面直线;AM与BN也是异面直线;AM与DD1是异面直线;BN与MB1也是异面直线,故①②错误,③④正确.
3.
已知m,n是不重合的直线,a,b分别垂直于两个不重合的平面α,β,有以下四个命题:
①若m⊥a,n∥b,且α⊥β,则m∥n.
②若m∥a,n∥b且α⊥β,则m⊥n.
③若m∥a,n⊥b且α∥β,则m⊥n.
④若m⊥a,n⊥b且α⊥β,则m∥n.
其中真命题的序号是 .
难度：
知识点：点 直线 平面之间的位置
使用次数：132
【答案】
:②③
【解析】
答案
4.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
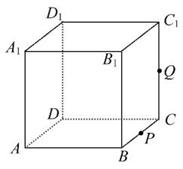①当0<CQ<
时,S为四边形.
②当CQ=时,S为等腰梯形.
③当CQ=
时,S与C1D1的交点R满足C1R=
.
④当<CQ<1时,S为六边形.
⑤当CQ=1时,S的面积为
.
难度：
知识点：空间几何体
使用次数：163
【答案】
①②③⑤【解析】①当0<CQ<时,截面如图1所示,截面是四边形APQM,故①正确.
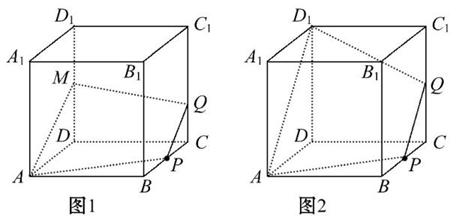
②当CQ=时,截面如图2所示,易知PQ∥AD1且PQ=AD1,S是等腰梯形,故②正确.
③当CQ=时,如图3.
作BF∥PQ交CC1的延长线于点F,则C1F=.作AE∥BF,交DD1的延长线于点E,D1E=,AE∥PQ,连接EQ交C1D1于点R,由于Rt△RC1Q∽Rt△RD1E,所以C1Q∶D1E=C1R∶RD1=1∶2,所以C1R=.
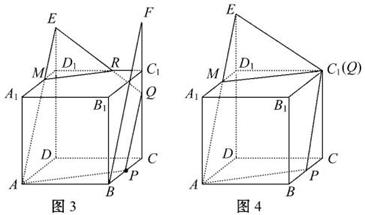
④当<CQ<1时,如图3,连接RM(点M为AE与A1D1的交点),显然S为五边形APQRM.
⑤当CQ=1时,如图4.
同③可作AE∥PQ交DD1的延长线于点E,交A1D1于点M,显然点M为A1D1的中点,所以S为菱形APQM,其面积为MP×AQ=×
×
=.
二、选择题 (共4题)
添加该题型下试题
1.
已知l,m是两条不同的直线,α,β是两个不同的平面,有下列五个命题:
①若l⊂β,且α∥β,则l∥α;
②若l⊥β,且α∥β,则l⊥α;
③若l⊥β,且α⊥β,则l∥α;
④α∩β=m,且l∥m,则l∥α;
⑤若α∩β=m,l∥α,l∥β,则l∥m.则所有正确命题的序号是( )
A.①③⑤ B.②④⑤
C.①②⑤ D.①②④
难度：
知识点：点 直线 平面之间的位置
使用次数：103
【答案】
C.根据面面平行的性质知,①②正确,⑤中由l∥α知,l平行平面α中的某条直线x,同理l平行平面β中的某条直线y,从而x∥y,所以y∥α,进而y∥m,故l∥m,所以⑤正确,故选C.
本卷还有7题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
12
总体难度：
中等
难度统计
难度系数
数量
占比
容易
7
58.33%
中等
5
41.66%
题型统计
大题类型
数量
占比
填空题
4
33.33%
选择题
4
33.33%
解答题
3
25.0%
综合题
1
8.33%
知识点统计
知识点
数量
占比
点 直线 平面之间的位置
9
75.0%
空间几何体
3
25.0%
版权提示
该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。