2013-2014学年 【课堂新坐标】（教师用书）高中数学 第3章 统计案例综合检测试卷及答案 苏教版选修2-3.doc
高中
整体难度：中等
2014-10-10
题号
一
二
三
四
五
评分
一、解答题 (共6题)
添加该题型下试题
1.
下表是收集到的新房屋的销售价格y和房屋的大小x的数据.
| 房屋的大小/m2 | 115 | 110 | 80 | 135 | 105 |
| 销售价格/万元 | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据的散点图；
(2)求y对x之间的线性回归方程，并在散点图中加上回归直线；
(3)此回归直线有意义吗？并回答回归系数的几何意义．
难度：
知识点：统计
使用次数：130
【答案】
【解】 (1)数据的散点图如图所示．
查表，n－2＝3时，临界值r0.05＝0.878，由|r|>r0.05知，变量y与x之间具有线性相关关系，回归直线是有意义的．
回归系数
＝0.196 2的几何意义是：房屋的大小每增大1 m2，新房屋的平均销售价格将提高0.196 2万元．
2.
随着我国经济的快速发展，城乡居民的生活水平不断提高，为研究某市家庭月平均收入与月平均生活支出的关系，该市统计部门随机调查了10个家庭，得数据如下：
| 家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 收入x (千元) | 0.8 | 1.1 | 1.3 | 1.5 | 1.5 | 1.8 | 2.0 | 2.2 | 2.4 | 2.8 |
| 支出y (千元) | 0.7 | 1.0 | 1.2 | 1.0 | 1.3 | 1.5 | 1.3 | 1.7 | 2.0 | 2.5 |
(1)判断家庭月平均收入与月平均生活支出是否相关？
(2)若二者线性相关，求回归直线方程．
难度：
知识点：统计
使用次数：161
【答案】
【解】 (1)作出散点图，如图所示．观察发现各个数据对应的点都在一条直线附近，所以二者呈线性相关关系．
(2)x＝
(0.8＋1.1＋1.3＋1.5＋1.5＋1.8＋2.0＋2.2＋2.4＋2.8)＝1.74，y＝(0.7＋1.0＋1.2＋1.0＋1.3＋1.5＋1.3＋1.7＋2.0＋2.5)＝1.42，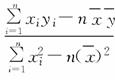
≈0.813 6，
＝1.42－1.74×0.813 6≈0.0043，∴回归方程为
＝0.813 6x＋0.004 3.
3.
对某校学生进行心理障碍测试得到如下列联表.
|
| 焦虑 | 说谎 | 懒惰 | 合计 |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 合计 | 25 | 20 | 65 | 110 |
试说明在这三种心理障碍中哪一种与性别关系最大？
难度：
知识点：统计
使用次数：103
【答案】
【解】 提出假设H0：焦虑、说谎、懒惰与性别无关．对于上述三种心理障碍分别构造三个随机变量χ
，χ
，χ
.由表中数据可得χ＝
≈0.863<2.706，χ＝
≈6.366>5.024，χ＝
≈1.410<2.706.所以没有充分的证据显示焦虑与性别有关，有97.5%的把握认为说谎与性别有关，没有充分的证据显示懒惰与性别有关．
4.
要分析学生初中升学的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽选10名学生分析他们入学的数学成绩和高一年级期末数学考试成绩，如下表所示．表中x是学生入学的数学成绩，y是高一年级期末考试数学成绩.
| x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
| y | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)画出散点图；
(2)求线性回归方程；
(3)若某学生王明亮的入学时的数学成绩为80分，试预测他在高一年级期末考试中的数学成绩为多少？
难度：
知识点：统计
使用次数：105
【答案】
【解】 (1)作出散点图如图所示，从散点图可以看出，这两个变量具有线性相关关系．
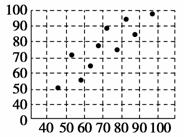
(2)可求得x＝(63＋67＋…＋76)＝70，y＝(65＋78＋…＋75)＝76.
＝
≈0.765 56，
＝76－0.765 56×70≈22.41，
所求的线性回归方程为
＝22.41＋0.765 56x.
(3)若学生王明亮入学成绩为80分，代入上面的线性回归方程＝22.41＋0.765 56x，可求得≈84(分)．
5.
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究，调查他们是否又发作过心脏病，调查结果如下表所示：
|
| 又发作过心脏病 | 未发作心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
试根据上述数据比较这两种手术对病人又发作心脏病的影响有没有差别．
难度：
知识点：统计
使用次数：130
【答案】
【解】 根据列联表中的数据，得到
χ2＝
≈1.78.
因为1.78<2.706.
所以我们没有理由说这两种手术对发作心脏病的影响有差别．
本卷还有15题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
20
总体难度：
中等
难度统计
难度系数
数量
占比
中等
12
60.0%
容易
8
40.0%
题型统计
大题类型
数量
占比
解答题
6
30.0%
填空题
13
65.0%
选择题
1
5.0%
知识点统计
知识点
数量
占比
统计
20
100.0%
版权提示
该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。