2015高中数学高考真题103694
高中
整体难度：中等
2014-12-01
题号
一
二
三
四
五
评分
一、选择题 (共16题)
添加该题型下试题
1.
已知E、F、G、H是空间内四个点，条件甲：E、F、G、H四点不共面，条件乙：直线EF和GH不相交，则甲是乙成立的( )
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
难度：
知识点：空间几何体
使用次数：144
【答案】
A
[解析] 点E、F、G、H四点不共面可以推出直线EF和GH不相交；但由直线EF和GH不相交不一定能推出E、F、G、H四点不共面，例如：EF和GH平行，这也是直线EF和GH不相交的一种情况，但E、F、G、H四点共面．故甲是乙成立的充分不必要条件．
2.
在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点，若EF与GH交于点M，则( )
A．M一定在AC上
B．M一定在BD上
C．M可能在AC上也可能在BD上
D．M不在AC上，也不在BD上
难度：
知识点：点 直线 平面之间的位置
使用次数：100
【答案】
[答案] A
[解析] 点M在平面ABC内，又在平面ADC内，故必在交线AC上．
3.
若直线l不平行于平面α，且l⊄α，则( )
A．α内的所有直线与l异面
B．α内不存在与l平行的直线
C．α内存在唯一的直线与l平行
D．α内的直线与l都相交
难度：
知识点：点 直线 平面之间的位置
使用次数：172
【答案】
B
[解析] 由题意知直线l与平面α相交，不妨设直线l∩α＝M，对A，在α内过M点的直线与l不异面，A错误；对B，假设存在与l平行的直线m，则由m∥l得l∥α，这与l∩α＝M矛盾，故B正确，C错误；对D，α内存在与l异面的直线，故D错误．综上知选B.
4.
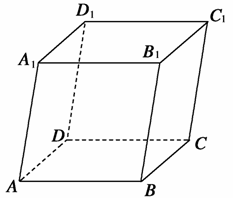
平行六面体ABCD－A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为( )
A．3 B．4
C．5 D．6
难度：
知识点：空间几何体
使用次数：156
【答案】
C
[解析] 如图，平行六面体ABCD－A1B1C1D1中，既与AB共面，也与CC1共面的棱为BC、C1D1、DC、AA1、BB1，共5条．
5.
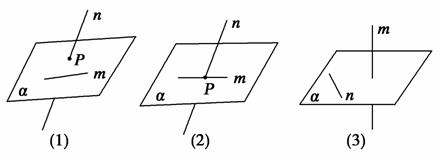
已知平面α和不重合的两条直线m、n，下列选项正确的是( )
A．如果m⊂α，n⊄α，m、n是异面直线，那么n∥α
B．如果m⊂α，n与α相交，那么m、n是异面直线
C．如果m⊂α，n∥α，m、n共面，那么m∥n
D．如果m⊥α，n⊥m，那么n∥α
难度：
知识点：点 直线 平面之间的位置
使用次数：194
【答案】
C
[解析] 如图(1)可知A错；如图(2)可知B错；如图(3)，m⊥α，n是α内的任意直线，都有n⊥m，故D错．
∵n∥α，∴n与α无公共点，∵m⊂α，∴n与m无公共点，又m、n共面，∴m∥n，故选C.
本卷还有23题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
28
总体难度：
中等
难度统计
难度系数
数量
占比
容易
15
53.57%
中等
13
46.42%
题型统计
大题类型
数量
占比
选择题
16
57.14%
填空题
6
21.42%
解答题
6
21.42%
知识点统计
知识点
数量
占比
空间几何体
5
17.85%
点 直线 平面之间的位置
23
82.14%
版权提示
该作品由: 用户赵云分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。