2004年普通高等学校招生全国统一考试数学试卷（上海卷.文）
高中
整体难度：偏难
2009-03-16
题号
一
二
三
四
五
评分
一、计算题 (共6题)
添加该题型下试题
1.
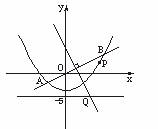
如图, 直线y=
x与抛物线y=
x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.
（1） 求点Q的坐标；
（2） 当P为抛物线上位于线段AB下方（含A、B） 的动点时, 求ΔOPQ面积的最大值.
难度：
知识点：圆锥曲线与方程
使用次数：115
【答案】
解：（1） 解方程 y=
x 得 x1=－4, x2=8
y=
x2－4 y1=－2, y2=4
即A（－4,－2）,B（8,4）, 从而AB的中点为M（2,1）.
由kAB==,直线AB的垂直平分线方程y－1=（x－2）.
令y=－5, 得x=5, ∴Q（5,－5）
（2） 直线OQ的方程为x+y=0, 设P（x, 
x2－4）.
∵点P到直线OQ的距离d=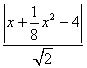
=
,
,∴SΔOPQ=
=
.
∵P为抛物线上位于线段AB下方的点, 且P不在直线OQ上,
∴－4≤x<4
－4或4－4<x≤8. ∵函数y=x2+8x－32在区间[－4,8] 上单调递增,
∴当x=8时, ΔOPQ的面积取到最大值30.
2.
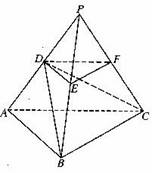如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.（棱长和是指多面体中所有棱的长度之和）
（1）证明：P-ABC为正四面体；
（2）若PD=
PA, 求二面角D-BC-A的大小；（结果用反三角函数值表示）
（3）设棱台DEF-ABC的体积为V, 是否存在体积为V且各棱长均相等的直平行六面体,
使得它与棱台DEF-ABC有相同的棱长和? 若存在,请具体构造出这样的一个直平行六面体,并给出证明；若不存在,请说明理由.
难度：
知识点：点 直线 平面之间的位置
使用次数：188
【答案】
证明：（1） ∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,
∴DE+EF+FD=PD+OE+PF. 又∵截面DEF∥底面ABC,
∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°, ∴P-ABC是正四面体.
解：（2）取BC的中点M,连拉PM,DM.AM.
∵BC⊥PM,BC⊥AM, ∴BC⊥平面PAM,BC⊥DM,
则∠DMA为二面角D-BC-A的平面角. 由（1）知,P-ABC的各棱长均为1,
∴PM=AM=
,由D是PA的中点, 得sin∠DMA=
,∴∠DMA=arcsin
.
（3）存在满足条件的直平行六面体. 棱台DEF-ABC的棱长和为定值6,体积为V.
设直平行六面体的棱长均为
,底面相邻两边夹角为α,
则该六面体棱长和为6, 体积为
sinα=V.
∵正四面体P-ABC的体积是
,∴0<V<,0<8V<1.可知α=arcsim（8V）
故构造棱长均为,底面相邻两边夹角为arcsim（8V）的直平行六面体即满足要求.
3.
设P1（x1,y1）, P1（x2,y2）,…, Pn（xn,yn）（n≥3,n∈N） 是二次曲线C上的点, 且a1=
2, a2=
2, …, an=
2构成了一个公差为d（d≠0） 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
（1）若C的方程为
－y2=1,n=3. 点P1（3,0） 及S3=162, 求点P3的坐标；（只需写出一个）
（2）若C的方程为y2=2px（p≠0）. 点P1（0,0）, 对于给定的自然数n, 证明：（x1+p）2, （x2+p）2, …,（xn+p）2成等差数列；
（3）若C的方程为
（a>b>0）. 点P1（a,0）, 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.
| 符号意义 | 本试卷所用符号 | 等同于《实验教材》符号 |
| 向量坐标 |
|
|
| 正切 | tg | tan |
难度：
知识点：点 直线 平面之间的位置
使用次数：127
【答案】
解：（1） a1=
2=9,由S3=
（a1+a3）=162,得a3=
3=99.
| 由 |
| ,得 | x |
| x | y |
∴点P3的坐标可以为（3
,3）.
（2）对每个自然数k,1≤k≤n,由题意
2=（k－1）d,及
| y | ,得x |
| x |
即（xk+p）2=p2+（k－1）d,
∴（x1+p）2, （x2+p）2, …,（xn+p）2是首项为p2,公差为d的等差数列.
（3） 解法一：原点O到二次曲线C:
（a>b>0）上各点的最小距离为b,最大距离为a.
∵a1=2=a2, ∴d<0,且an=
2=a2+（n－1）d≥b2,
∴
≤d<0. ∵n≥3,
>0
∴Sn=na2+d在[,0）上递增,
故Sn的最小值为na2+・=
.
解法二：对每个自然数k（2≤k≤n）,
| 由 | x | ,解得y |
|
|
∵0< y
≤b2,得
≤d<0 ∴≤d<0 以下与解法一相同.
4.
已知复数z1满足（1+i）z1=－1+5i, z2=a－2－i, 其中i为虚数单位,a∈R, 若
<
,求a的取值范围.
难度：
知识点：数系的扩充与复数的引入
使用次数：111
【答案】
解：由题意得 z1=
=2+3i,
于是
=
=
,
=
.
<,得a2－8a+7<0,1<a<7.
5.
某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y（单位：m）的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少（精确到0.001m） 时用料最省?
难度：
知识点：函数的应用
使用次数：113
【答案】
解：由题意得xy+
x2=8, ∴y=
=
（0<x<4
）.
于定, 框架用料长度为 l=2x+2y+2（
）=（
+
）x+
≥4
.
当（+）x=,即x=8－4时等号成立.
此时, x≈2.343,y=2≈2.828. 故当x为2.343m,y为2.828m时, 用料最省.
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
22
100.0%
题型统计
大题类型
数量
占比
计算题
6
27.27%
填空题
12
54.54%
选择题
4
18.18%
知识点统计
知识点
数量
占比
圆锥曲线与方程
3
13.63%
点 直线 平面之间的位置
3
13.63%
函数的应用
8
36.36%
常用逻辑用语
1
4.54%
导数及其应用
1
4.54%
平面向量
1
4.54%
圆与方程
1
4.54%
概率
1
4.54%
数列
1
4.54%
三角函数
1
4.54%
数系的扩充与复数的引入
1
4.54%
版权提示
该作品由: 用户李超分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。