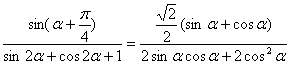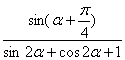(向量a、b满足(a-b)・(2a+b)=-4,且|a|=2,|b|=4,则a与b夹角的余弦值等于 .
―1/2
某同学参加科普知识竞赛,需回答3个问题.竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(Ⅰ)求这名同学得300分的概率;
(Ⅱ)求这名同学至少得300分的概率.
解:记“这名同学答对第i个问题”为事件![]() ,则
,则
P(A1)=0.8,P(A2)=0.7,P(A3)=0.6.
(Ⅰ)这名同学得300分的概率
P1=P(A1![]() A3)+P(
A3)+P(![]() A2A3)
A2A3)
=P(A1)P(![]() )P(A3)+P(
)P(A3)+P(![]() )P(A2)P(A3)
)P(A2)P(A3)
=0.8×0.3×0.6+0.2×0.7×0.6
=0.228.
(Ⅱ)这名同学至少得300分的概率
P2=P1+P(A1A2A3)
=0.228+P(A1)P(A2)P(A3)
=0.228+0.8×0.7×0.6
=0.564.
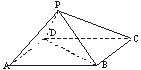 如图,四棱锥P―ABCD中,底面ABCD为矩形,AB=8,AD=4
如图,四棱锥P―ABCD中,底面ABCD为矩形,AB=8,AD=4![]() ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
(Ⅰ)求四棱锥P―ABCD的体积;
(Ⅱ)证明PA⊥BD.
本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析问题的能力.
解:(Ⅰ)如图1,取AD的中点E,连结PE,则PE⊥AD.

图1
作PO⊥平面ABCD,垂足为O,连结OE.
根据三垂线定理的逆定理得OE⊥AD,
所以∠PEO为侧面PAD与底面所成二面角的平面角.
由已知条件可知∠PEO=60°,PE=6,
所以PO=3![]() ,
,
四棱锥P-ABCD的体积
VP-ABCD=![]()
(Ⅱ)解法一:如图1,以O为原点建立空间直角坐标系.通过计算可得
P(0,0,3![]() ),A(2
),A(2![]() ,-3,0),B(2
,-3,0),B(2![]() ,5,0),D(-2
,5,0),D(-2![]() ,-3,0).
,-3,0).
所以![]() =(2
=(2![]() ,-3,-3
,-3,-3![]() ),
), ![]() =(-4
=(-4![]() ,-8,0).
,-8,0).
因为![]() ・
・![]() =-24+24+0=0,
=-24+24+0=0,
所以PA⊥BD.
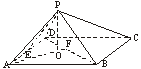
图2
解法二:如图2,连结AO,并延长AO交BD于点F.通过计算可得
EO=3,AE=2![]() ,又由AD=4
,又由AD=4![]() ,AB=8,
,AB=8,
得 ![]() .
.
所以 Rt△AEO∽Rt△BAD,
得 ∠EAO=∠ABD.
所以 ∠EAO+∠ADF=90°,
所以 AF⊥BD.
因为AF为PA在平面ABCD内的射影,
所以 PA⊥BD.

该作品由: 用户闫璟鹏分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。