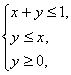2004年普通高等学校招生全国统一考试数学试卷（全国卷.理）
高中
整体难度：偏难
2009-03-16
题号
一
二
三
四
五
评分
一、填空题 (共2题)
添加该题型下试题
二、计算题 (共3题)
添加该题型下试题
1.
已知数列{
}为等比数列，
（Ⅰ）求数列{}的通项公式；
（Ⅱ）设
是数列{}的前
项和，证明
难度：
知识点：数列
使用次数：172
【答案】
解：（I）设等比数列{an}的公比为q，则a2=a1q, a5=a1q4.
a1q=6,
依题意，得方程组 a1q4=162.
解此方程组，得a1=2, q=3.
故数列{an}的通项公式为an=2・3n－1.
（II） 
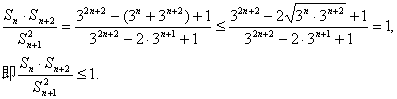
2.
已知直线
为曲线
在点（1，0）处的切线，
为该曲线的另一条切线，且
（Ⅰ）求直线的方程；
（Ⅱ）求由直线、和
轴所围成的三角形的面积.
难度：
知识点：点 直线 平面之间的位置
使用次数：107
【答案】
解：（Ⅰ）y′=2x+1.
直线l1的方程为y=3x－3.
设直线l2过曲线y=x2+x－2上 的点B（b, b2+b－2）,则l2的方程为y=(2b+1)x－b2－2
因为l1⊥l2，则有2b+1=
所以直线l2的方程为
（II）解方程组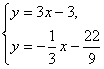
得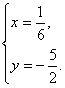
所以直线l1和l2的交点的坐标为
l1、l2与x轴交点的坐标分别为（1，0）、
.
所以所求三角形的面积 
3.
双曲线
的焦距为2c，直线
过点（a，0）和（0，b），且点（1，0）到直线的距离与点（－1，0）到直线的距离之和
求双曲线的离心率e的取值范围.
难度：
知识点：圆锥曲线与方程
使用次数：177
【答案】
解：直线
的方程为
，即 
由点到直线的距离公式，且
，得到点（1，0）到直线的距离
，
同理得到点（－1，0）到直线的距离
由
即 
于是得 
解不等式，得 
由于
所以
的取值范围是
三、选择题 (共14题)
添加该题型下试题
本卷还有14题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
19
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
19
100.0%
题型统计
大题类型
数量
占比
填空题
2
10.52%
计算题
3
15.78%
选择题
14
73.68%
知识点统计
知识点
数量
占比
三角函数
4
21.05%
不等式
1
5.26%
数列
2
10.52%
点 直线 平面之间的位置
3
15.78%
圆锥曲线与方程
2
10.52%
常用逻辑用语
1
5.26%
函数的应用
4
21.05%
圆与方程
1
5.26%
高考试题
1
5.26%
版权提示
该作品由: 用户俞鸿文分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。