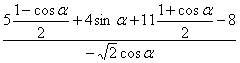2006年普通高等学校招生全国统一考试数学试卷（安徽卷.理）
高中
整体难度：中等
2009-03-16
题号
一
二
三
四
五
评分
一、填空题 (共1题)
添加该题型下试题
1.
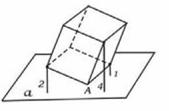
多面体上，位于同一条棱两端的顶点称为相邻的，如图，正方体的一个顶点A在平面
内，其余顶点在的同侧，正方体上与顶点A相邻的三个顶点到的距离分别为1，2和4，P是正方体的其余四个顶点中的一个，则P到平面的距离可能是：
①3； ②4； ③5； ④6； ⑤7
以上结论正确的为______________。（写出所有正确结论的编号）
难度：
知识点：点 直线 平面之间的位置
使用次数：160
【答案】
①③④⑤
二、计算题 (共3题)
添加该题型下试题
=
=
=
2.
在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时，需要选用两种不同的添加剂。现有芳香度分别为0，1，2，3，4，5的六种添加剂可供选用。根据试验设计原理，通常首先要随机选取两种不同的添加剂进行搭配试验。用
表示所选用的两种不同的添加剂的芳香度之和。
（Ⅰ）写出的分布列；（以列表的形式给出结论，不必写计算过程）
（Ⅱ）求的数学期望E。（要求写出计算过程或说明道理）
难度：
知识点：概率
使用次数：154
【答案】
解：（Ⅰ）
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| P |
|
|
|
|
|
|
|
|
|
（Ⅱ）
3.
数列
的前
项和为
，已知
（Ⅰ）写出与
的递推关系式（
），并求关于的表达式；
（Ⅱ）设
，求数列
的前项和
。
难度：
知识点：数列
使用次数：137
【答案】
解：由
得：
，即
，所以
，对
成立。
由，
，…，
相加得：
，又
，所以
，当
时，也成立。
（Ⅱ）由
，得
。
而
，
，
三、综合题 (共1题)
添加该题型下试题
1.
已知函数
在R上有定义，对任何实数
和任何实数
，都有
（Ⅰ）证明
；
（Ⅱ）证明
其中
和
均为常数；
（Ⅲ）当（Ⅱ）中的
时，设
，讨论
在（
）内的单调性并求极值。
难度：
知识点：函数的应用
使用次数：153
【答案】
证明（Ⅰ）令
，则
，∵
，∴
。
（Ⅱ）①令
，∵，∴
，则
。
假设
时，
，则
，而
，
∴，即
成立。
②令
，∵，∴
，
假设时
，则
，而
，
∴，即
成立。
∴
成立。
（Ⅲ）当时，
，
令
，得
；
当
时，
，∴
是单调递减函数；
当
时，
，∴是单调递增函数；
所以当
时，函数在
内取得极小值，极小值为
四、选择题 (共17题)
添加该题型下试题
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
中等
难度统计
难度系数
数量
占比
偏难
2
9.09%
容易
3
13.63%
中等
12
54.54%
基础
5
22.72%
题型统计
大题类型
数量
占比
填空题
1
4.54%
计算题
3
13.63%
综合题
1
4.54%
选择题
17
77.27%
知识点统计
知识点
数量
占比
点 直线 平面之间的位置
2
9.09%
三角函数
4
18.18%
概率
2
9.09%
函数的应用
5
22.72%
数列
1
4.54%
直线与方程
1
4.54%
空间几何体
1
4.54%
不等式
1
4.54%
集合与函数的概念
2
9.09%
圆锥曲线与方程
1
4.54%
常用逻辑用语
1
4.54%
数系的扩充与复数的引入
1
4.54%
版权提示
该作品由: 用户王华东分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。