2015高中数学高考真题112262
高中
整体难度:中等
2015-09-14
题号
一
二
三
四
五
评分
一、解答题 (共8题)
添加该题型下试题
难度:
知识点:不等式
使用次数:131
【答案】
【解析】如图,阴影部分为可行域,交点坐标分别为
![]() ,
,
(1)区域![]() 的面积为
的面积为![]()
(2)∵直线![]() 恒过定点
恒过定点![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴实数![]() 的取值范围
的取值范围![]()
2.
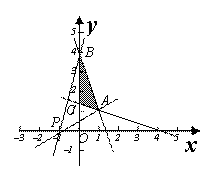
设![]() 满足约束条件
满足约束条件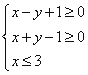 ,求
,求![]() 的最小值与最大值
的最小值与最大值
难度:
知识点:不等式
使用次数:160
【答案】
【略解】不等式组表示的平面区域的角点坐标分别为![]() ,
,
![]() ,故
,故![]() 的最小值为-6与最大值为
的最小值为-6与最大值为![]()
变式:设![]() 满足约束条件
满足约束条件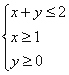 ,求
,求![]() 的最小值与最大值
的最小值与最大值
3.
某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克,![]() 原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗
原料1千克。每桶甲产品的利润是300元,每桶乙产品的利润是400元。公司在生产这两种产品的计划中,要求每天消耗![]() 、
、![]() 原料都不超过12千克。该公司应如何通过合理安排生产计划,才能使公司获得最大的利润,最大利润是多少元?
原料都不超过12千克。该公司应如何通过合理安排生产计划,才能使公司获得最大的利润,最大利润是多少元?
难度:
知识点:不等式
使用次数:175
【答案】
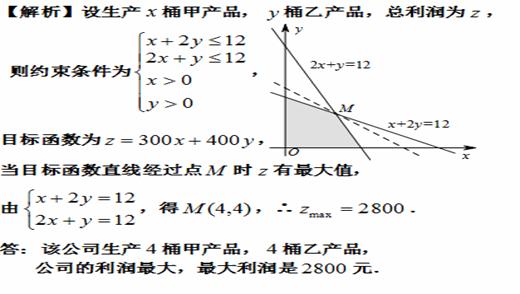
4.
若![]() 满足约束条件
满足约束条件 ,求
,求![]() 的最小值与最大值
的最小值与最大值
难度:
知识点:不等式
使用次数:163
【答案】
 【解析】如图,阴影部分为可行域,
【解析】如图,阴影部分为可行域,![]() ,
,
令![]() ,则
,则![]() 表示以
表示以![]() 为圆心的半径的平方
为圆心的半径的平方
当这个圆过点 ![]() 时,半径最小,
时,半径最小,![]()
当这个圆过点 ![]() 时,半径最小,
时,半径最小,![]()
∴![]() .
.![]()
所以![]() 的最小值为2,最大值为
的最小值为2,最大值为![]()
本卷还有6题,登录并加入会员即可免费使用哦~
立即下载
全选试题
编辑试卷
收藏试卷

试题总数:
11
总体难度:
中等
难度统计
难度系数
数量
占比
中等
6
54.54%
容易
5
45.45%
题型统计
大题类型
数量
占比
解答题
8
72.72%
填空题
2
18.18%
选择题
1
9.09%
知识点统计
知识点
数量
占比
不等式
11
100.0%
版权提示
该作品由: 用户流星分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。