2008江苏高三上学期苏教版高中数学期末考试4636
高中
整体难度：中等
2009-03-16
题号
一
二
三
四
五
评分
一、计算题 (共6题)
添加该题型下试题
1.
如图，AB是⊙O的直径，CD是⊙O的切线，C是切点，AD交⊙O于点E，AC=
，CD=1，AC平分∠BAA。
（1）求证：AD⊥CD；
（2）求AB的长。
难度：
知识点：几何证明选讲
使用次数：67
【答案】
解：（1）连结BC
∵AB是⊙O的直径，
∴∠ACB=90°。
∵CD是⊙O的切线，AD交⊙O于点E，
∴∠ACD=∠ABC。
∵AC平分∠BAD
∴∠CAD=∠BAC。
∴△ACD∽△ABC
∴∠ADC=∠ACB=90°
∴AD⊥CD。
（2）∵△ACD∽△ABC
∴
∵AC=
∴AD=2
∴
2.
二阶矩阵M1和M2对应的变换对正方形区域的作用结果如下图所示：
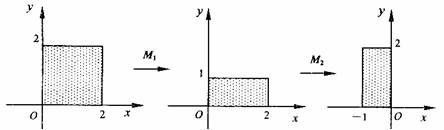
（1）分别写出一个满足条件的矩阵M1和M2；
（2）根据（1）的结果，令M=M2M1，求曲线x－y－1=0在矩阵M对应的变换作用下的曲线的方程。
难度：
知识点：矩阵与变换
使用次数：188
【答案】
解：（1）M1=
（2）∴M=
设直线
上任意一点P（x0,y0）是在M对应的变换作用下的对应点P′（x,y）。
∴所求的曲线方程为
3.
已知⊙O1和⊙O2的极坐标方程分别是
，（a是非零常数）。
（1）将两圆的极坐标方程化为直角坐标方程；
（2）若两圆的圆心距为
，求a的值。
难度：
知识点：坐标系与参数方程
使用次数：61
【答案】
解：（1）两圆的极坐标方程可化为
∴两圆的直角坐标方程是
（2）根据（1）可知道两圆心的直角坐标是O1（1，0）和O2（0，a）
4.
设函数
（1）解不等式
；
（2）若
的取值范围。
难度：
知识点：不等式选讲
使用次数：77
【答案】
解：（1）∵
∴当x<1时，3－2x>3，解得x<0；
当1
无解
当x>2时2x－3>3，解得x<3.
综上，x<0或x>3，
∴不等式f（x）>3的解集为
（2）∵
∴
∵
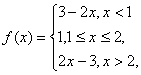
恒成立
∴a<1，即实数a的取值范围是
5.
某单位举行抽奖活动，每个员工有一次抽奖机会，抽奖箱中放有6个相同的乓乒球，其中三个球上标有数字1，两个球上标有数字2，还有一个球上标有数字3，每个抽奖者从中一次抽出两个球，记两个球上所标数字的和为X，奖项及相应奖品价值如下表：
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| X | 5 | 4或3 | 2 |
| 奖品价值 | 200 | 100 | 50 |
（1）求某员工获一等奖的概率；
（2）求某员工所获奖品价值Y（元）的概率分布；
（3）该单位共有员工30人，试估计该单位需要准备价值多少元的奖品？
难度：
知识点：概率
使用次数：113
【答案】
解：（1）某员工获得一等奖的概率为
（2）∵某员工获三等奖的概率为
获二等奖的概率为
∴某员工所获奖品价值Y（无）的概率分布为：
| Y | 200 | 100 | 50 |
| P |
|
|
|
（3）EY=200×
+100×
+50×
=
∴该单位需准备奖品的价值约为
元
本卷还有1题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
6
总体难度：
中等
难度统计
难度系数
数量
占比
中等
4
66.66%
容易
2
33.33%
题型统计
大题类型
数量
占比
计算题
6
100.0%
知识点统计
知识点
数量
占比
几何证明选讲
1
16.66%
矩阵与变换
1
16.66%
坐标系与参数方程
1
16.66%
不等式选讲
1
16.66%
概率
1
16.66%
圆锥曲线与方程
1
16.66%
版权提示
该作品由: 用户杨慧莲分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。