2015河南高二上学期高中数学期末考试116157
高中
整体难度：中等
2016-02-29
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
下列命题错误的是（ ）
A．命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2≠0”
B．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件
C．若p∧q为假命题，则p、q均为假命题
D．对于命题p：∃x∈R，x2+x+1＜0，则￢p：∀x∈R，x2+x+1≥0
难度：
知识点：常用逻辑用语
使用次数：190
【答案】
C【考点】复合命题的真假．
【专题】常规题型．
【分析】A．逆否命题 条件结论都否定后位置互换
B，x＞2可推出x2﹣3x+2＞0成立，但x2﹣3x+2＞0等价于x＞2或x＜1
通过分析可得A，B，D均正确．
【解答】解：∵若p则q的逆否命题是若非q，则非p，∴命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2≠0”是真命题
∵x2﹣3x+2＞0⇔x＞2或x＜1，∴x＞2⇒x2﹣3x+2＞0∴B是真命题
∵全称命题的否定特称命题，对于命题p：∃x∈R，x2+x+1＜0，则¬p：∀x∈R，x2+x+1≥0，∴C是真命题．
∵p∧q一假即为假，∴C答案错误．
故选C
【点评】本题考查了四种命题，复合命题的真假，充要条件以及全称命题的否定．注意审题．
2.
在△ABC中，三边a，b，c所对的角分别为A，B，C，若a2+b2=
ab+c2，则角C为（ ）
A．30° B．45° C．150° D．135°
难度：
知识点：解三角形
使用次数：133
【答案】
B【考点】余弦定理．
【专题】计算题．
【分析】利用余弦定理可求得cosC=
，从而可求得角C的值．
【解答】解：∵在△ABC中，由余弦定理a2+b2=c2+2abcosC，
又a2+b2=
ab+c2，
∴cosC=，
∴C=45°
故选B．
【点评】本题考查余弦定理，求得cosC=是关键，突出整体代入的思想，属于基础题．
3.
不等式ax2﹣2x+1＜0的解集非空的一个必要而不充分条件是（ ）
A．a＜1 B．a＜0 C．0＜a＜1 D．a≤1
难度：
知识点：不等式
使用次数：176
【答案】
D【考点】必要条件、充分条件与充要条件的判断．
【专题】计算题．
【分析】通过对二次项系数分类讨论求出不等式ax2﹣2x+1＜0的解集非空的充要条件，必要而不充分条件的a的范围应该比a＜1的范围大；得到选项．
【解答】解：要使不等式ax2﹣2x+1＜0的解集非空
当a=0时，不等式为﹣2x+1＜0，其解集为x＞
；
当a＞0时，△=4﹣4a＞0即0＜a＜1；
当a＜0时，满足不等式ax2﹣2x+1＜0的解集非空；
所以不等式ax2﹣2x+1＜0的解集非空的充要条件为a＜1；
所以不等式ax2﹣2x+1＜0的解集非空的一个必要而不充分条件应该比a＜1的范围大；
故选D．
【点评】解决二次不等式的问题，应该注意二次项系数为字母时，应该对其分类讨论，是高考常考的题型，属于中档题．
4.
等差数列{an}公差不为零，首项a1=1，a1，a2，a5是等比数列，则数列{an}的前10项和是（ ）
A．90 B．100 C．145 D．190
难度：
知识点：数列
使用次数：181
【答案】
B【考点】等比数列的通项公式；等差数列的通项公式；等差数列的前n项和．
【专题】等差数列与等比数列．
【分析】由a1=1，a1、a2、a5成等比数列，可得a22=a1a5，由等差数列的通项公式可得（1+d）2=1×（1+4d），从而可求得d，根据等差数列的前n项和公式可求的答案．
【解答】解：设等差数列{an}的公差为d，则d≠0，
∵a1，a2，a5成等比数列，
∴a22=a1a5，
又∵首项a1=1，
∴（1+d）2=1×（1+4d），即d（d﹣2）=0，
∵d≠0，
∴d=2，
∴
=100．
故选：B．
【点评】本题考查了等差数列与等比数列的综合应用，等差数列和等比数列是数列内容中的最基本的数列，是高考的热点之一，解决问题的关键是要熟练掌握公式，灵活应用公式．属于基础题．
5.
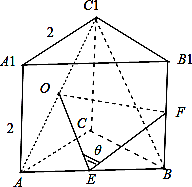
在直三棱柱ABC﹣A1B1C1中，AC=AA1=2，∠ACB=90°，点E，F分别是棱AB，BB1的中点，当二面角C1﹣AA1﹣B为45°时，直线EF与BC1的夹角为（ ）
A．60° B．45° C．90° D．120°
难度：
知识点：直线与方程
使用次数：103
【答案】
C【考点】两直线的夹角与到角问题．
【专题】转化思想；综合法；直线与圆；空间角．
【分析】先将EF平移到AB1，再利用中位线进行平移，使两条异面直线移到同一点，得到直线EF和BC1所成的角，求之即可．
【解答】解：由题意可得∠CAB=45°为二面角C1﹣AA1﹣B的平面角，△ABC为等腰直角三角形，
连AC1，取AC1得中点O，∵E，F分别是棱AB，BB1的中点，∴OE平行且等于BC1，
∠OEF=θ或其补角，即为直线EF与BC1的夹角．
由于OE=BC1=
，EF=
=
=
，OF=
=
，
由余弦定理可得cosθ=
=0，
∴θ=90°，
故选：C．
【点评】本题主要考查了异面直线及其所成的角，平移法是研究异面直线所成的角的最常用的方法，经常考查，属于中档题．
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
中等
难度统计
难度系数
数量
占比
中等
11
50.0%
容易
11
50.0%
题型统计
大题类型
数量
占比
选择题
12
54.54%
填空题
4
18.18%
解答题
6
27.27%
知识点统计
知识点
数量
占比
常用逻辑用语
2
9.09%
解三角形
4
18.18%
不等式
3
13.63%
数列
4
18.18%
直线与方程
1
4.54%
点 直线 平面之间的位置
2
9.09%
圆锥曲线与方程
4
18.18%
空间几何体
1
4.54%
平面向量
1
4.54%
版权提示
该作品由: 用户詹百灵分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。