2017届江苏省南京市、盐城市高三第一次模拟 数学考试试卷及答案
高中
整体难度：中等
2017-02-26
题号
一
二
三
四
五
评分
一、解答题 (共11题)
添加该题型下试题
2.
在平面直角坐标系
中，已知直线
为参数). 现以坐标原点
为极点，以
轴非负半轴为极轴建立极坐标系，设圆
的极坐标方程为
，直线
与圆交于
两点，求弦
的长.
难度：
知识点：坐标系与参数方程
使用次数：113
【答案】
、解：直线为参数)化为普通方程为
，
圆的极坐标方程化为直角坐标方程为
， …………4分
则圆的圆心到直线l的距离为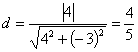
，
所以
.
4.
如图，是半圆的直径，点
为半圆外一点，
分别交半圆于点
.若
，
，
，求
的长.
 |
难度：
知识点：几何证明选讲
使用次数：151
【答案】
解：由切割线定理得：
则
，解得
，
又因为是半圆的直径，故
,
则在三角形PDB中有
. …
5.
若存在常数
、
、
，使得无穷数列
满足
则称数列为“段比差数列”，其中常数
、、分别叫做段长、段比、段差. 设数列
为“段比差数列”.
（1）若的首项、段长、段比、段差分别为1、3、、3.
①当
时，求
；
②当
时，设的前
项和为
，若不等式
对
恒成立，求实数
的取值范围；
（2）设为等比数列，且首项为
，试写出所有满足条件的，并说明理由.
难度：
知识点：数列
使用次数：158
【答案】
．（1）①方法一：∵的首项、段长、段比、段差分别为1、3、0、3，
，
，
. ……………3分
方法二：∵的首项、段长、段比、段差分别为1、3、0、3，
∴
，
，
，
，
，
，
，…
∴当
时，是周期为3的周期数列.
∴
. ……………3分
②方法一：∵的首项、段长、段比、段差分别为1、3、1、3，
∴
，
∴
是以为首项、6为公差的等差数列，
又
，
， ……………6分
，
，设
，则
，
又
，
当
时，
，
；当
时，
，
，
∴
，∴
， ……………9分
∴
，得
. ……………10分
方法二：∵的首项、段长、段比、段差分别为1、3、1、3，
∴
，∴
，∴
是首项为、公差为6的等差数列，
∴
，
易知中删掉的项后按原来的顺序构成一个首项为1公差为3的等差数列，
，
， ………………6分
以下同方法一.
（2）方法一：设的段长、段比、段差分别为、、，
则等比数列的公比为
，由等比数列的通项公式有
，
当
时，
，即
恒成立， ……………12分
①若，则
，
；
②若
，则
，则
为常数，则
，为偶数，
，
；
经检验，满足条件的的通项公式为或. ……………16分
方法二：设的段长、段比、段差分别为、、，
①若
，则
，
，
，
，
由
，得
；由
，得
，
联立两式，得
或
，则或，经检验均合题意. …………13分
②若
，则，，
，
由，得
，得，则，经检验适合题意.
综上①②，满足条件的的通项公式为或. …
本卷还有21题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
26
总体难度：
中等
难度统计
难度系数
数量
占比
中等
14
53.84%
偏难
1
3.84%
容易
11
42.30%
题型统计
大题类型
数量
占比
解答题
11
42.30%
综合题
1
3.84%
填空题
14
53.84%
知识点统计
知识点
数量
占比
不等式
2
7.69%
坐标系与参数方程
1
3.84%
数列与差分
1
3.84%
几何证明选讲
1
3.84%
数列
2
7.69%
基本初等函数I
2
7.69%
解三角形
3
11.53%
圆与方程
1
3.84%
点 直线 平面之间的位置
1
3.84%
推理与证明
1
3.84%
平面向量
1
3.84%
空间几何体
1
3.84%
三角函数
1
3.84%
圆锥曲线与方程
1
3.84%
概率
2
7.69%
框图
1
3.84%
统计
1
3.84%
数系的扩充与复数的引入
1
3.84%
集合与函数的概念
1
3.84%
计数原理
1
3.84%
版权提示
该作品由: 用户84359738分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。