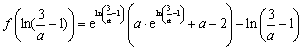已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集包含
的解集包含![]() ,求
,求![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,是开口向下,对称轴
,是开口向下,对称轴![]() 的二次函数.
的二次函数.
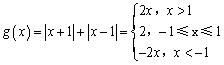 ,
,
当![]() 时,令
时,令![]() ,解得
,解得![]()
![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减
上单调递减
∴此时![]() 解集为
解集为![]() .
.
当![]() 时,
时,![]() ,
,![]() .
.
当![]() 时,
时,![]() 单调递减,
单调递减,![]() 单调递增,且
单调递增,且![]() .
.
综上所述,![]() 解集
解集![]() .
.
(2)依题意得:![]() 在
在![]() 恒成立.
恒成立.
即![]() 在
在![]() 恒成立.
恒成立.
则只须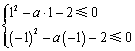 ,解出:
,解出:![]() .
.
故![]() 取值范围是
取值范围是![]() .
.
已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
已知椭圆![]() :
:![]()
![]() ,四点
,四点![]() ,
,![]() ,
,![]() ,
,![]() 中恰有三点在椭圆
中恰有三点在椭圆![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率的和为
的斜率的和为![]() ,证明:
,证明:![]() 过定点.
过定点.
(1)根据椭圆对称性,必过![]() 、
、![]()
又![]() 横坐标为1,椭圆必不过
横坐标为1,椭圆必不过![]() ,所以过
,所以过![]() 三点
三点
将![]() 代入椭圆方程得
代入椭圆方程得
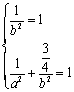 ,解得
,解得![]() ,
,![]()
∴椭圆![]() 的方程为:
的方程为:![]() .
.
(2)![]() 当斜率不存在时,设
当斜率不存在时,设![]()
![]()
得![]() ,此时
,此时![]() 过椭圆右顶点,不存在两个交点,故不满足.
过椭圆右顶点,不存在两个交点,故不满足.
![]() 当斜率存在时,设
当斜率存在时,设![]()
![]()
联立![]() ,整理得
,整理得![]()
![]() ,
,![]()
则![]()
![]()
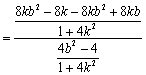
![]() 又
又![]()
![]() ,此时
,此时![]() ,存在
,存在![]() 使得
使得![]() 成立.
成立.
∴直线![]() 的方程为
的方程为![]()
当![]() 时,
时,![]()
所以![]() 过定点
过定点![]() .
.
为了抽检某种零件的一条生产线的生产过程,实验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示一天内抽取的16个零件中其尺寸在
表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及
及![]() 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(I)试说明上述监控生产过程方法的合理性:
(II)下面是检验员在一天内抽取的16个零件的尺寸:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
经计算得![]() ,
,![]() ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸,![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查,剔除
,利用估计值判断是否需对当天的生产过程进行检查,剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到
(精确到![]() ).
).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() .
.
![]() ,
,![]() .
.
(1)由题可知尺寸落在![]() 之内的概率为
之内的概率为![]() ,落在
,落在![]() 之外的概率为
之外的概率为![]() .
.
![]()
![]()
由题可知![]()
![]()
(2)(i)尺寸落在![]() 之外的概率为
之外的概率为![]() ,
,
由正态分布知尺寸落在![]() 之外为小概率事件,
之外为小概率事件,
因此上述监控生产过程的方法合理.
(ii)
![]()
![]()
![]()
![]() ,
,![]() 需对当天的生产过程检查.
需对当天的生产过程检查.
因此剔除![]()
剔除数据之后:![]() .
.
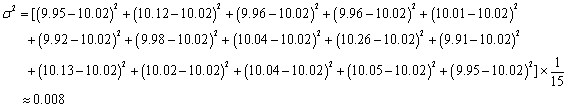
![]()
如图,在四棱锥![]() 中,
中,![]() 中,且
中,且![]() .
.
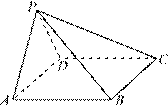
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(1)证明:∵![]()
∴![]() ,
,![]()
又∵![]()
 ,∴
,∴![]()
又∵![]() ,
,![]() 、
、![]() 平面
平面![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
∴平面![]() 平面
平面![]()
(2)取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]() ,
,![]()
∵![]()
![]()
![]()
![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
![]()
![]()
由(1)知,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,又
,又![]() 、
、![]() 平面
平面![]()
∴![]() ,
,![]()
又∵![]() ,∴
,∴![]()
∴![]() 、
、![]() 、
、![]() 两两垂直
两两垂直
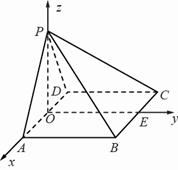
∴以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]()
设![]() ,∴
,∴![]() 、
、![]() 、
、![]() 、
、![]() ,
,
∴![]() 、
、![]() 、
、![]()
设![]() 为平面
为平面![]() 的法向量
的法向量
由![]() ,得
,得![]()
令![]() ,则
,则![]() ,
,![]() ,可得平面
,可得平面![]() 的一个法向量
的一个法向量![]()
∵![]() ,∴
,∴![]()
又知![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ,又
,又![]()
∴![]() 平面
平面![]()
即![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]()
∴![]()
由图知二面角![]() 为钝角,所以它的余弦值为
为钝角,所以它的余弦值为![]()
本卷还有18题,登录并加入会员即可免费使用哦~

该作品由: 用户黄河分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。