设![]() 和
和![]() 是两个等差数列,记
是两个等差数列,记![]()
![]() ,
,
其中![]() 表示
表示![]() 这
这![]() 个数中最大的数.
个数中最大的数.
(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的值,并证明
的值,并证明![]() 是等差数列;
是等差数列;
(Ⅱ)证明:或者对任意正数![]() ,存在正整数
,存在正整数![]() ,当
,当![]() 时,
时,![]() ;或者存在正整数
;或者存在正整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)分别代入求![]() ,观察规律,再证明当
,观察规律,再证明当![]() 时,
时,![]() ,所以
,所以![]() 关于
关于![]() 单调递减. 所以
单调递减. 所以![]() ,即证明;(Ⅱ)首先求
,即证明;(Ⅱ)首先求![]() 的通项公式,分
的通项公式,分![]() 三种情况讨论证明.
三种情况讨论证明.

(Ⅱ)设数列![]() 和
和![]() 的公差分别为
的公差分别为![]() ,则
,则
![]() .
.
所以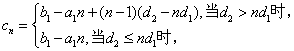
①当![]() 时,取正整数
时,取正整数![]() ,则当
,则当![]() 时,
时,![]() ,因此
,因此![]() .
.
此时,![]() 是等差数列.
是等差数列.
②当![]() 时,对任意
时,对任意![]() ,
,
![]()
此时,![]() 是等差数列.
是等差数列.
③当![]() 时,
时,
当![]() 时,有
时,有![]() .
.
所以![]()
![]()
对任意正数![]() ,取正整数
,取正整数![]() ,
,
故当时,![]() .
.
【考点】1.新定义;2.数列的综合应用;3.推理与证明.
【名师点睛】近年北京卷理科压轴题一直为新信息题,本题考查学生对新定义的理解能力和使用能力,本题属于偏难问题,反映出学生对于新的信息的的理解和接受能力,本题考查数列的有关知识及归纳法证明方法,即考查了数列(分段形函数)求值,又考查了归纳法证明和对数据的分析研究,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题,特别是第二两步难度较大,适合选拔优秀学生.
已知抛物线C:y2=2px过点P(1,1).过点(0,![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
(Ⅰ)方程为![]() ,抛物线C的焦点坐标为(
,抛物线C的焦点坐标为(![]() ,0),准线方程为
,0),准线方程为![]() .(Ⅱ)详见解析.
.(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)代入点![]() 求得抛物线的方程,根据方程表示焦点坐标和准线方程;(Ⅱ)设直线l的方程为
求得抛物线的方程,根据方程表示焦点坐标和准线方程;(Ⅱ)设直线l的方程为![]() (
(![]() ),与抛物线方程联立,得到根与系数的关系,直线ON的方程为
),与抛物线方程联立,得到根与系数的关系,直线ON的方程为![]() ,联立求得点
,联立求得点![]() 的坐标
的坐标![]() ,证明
,证明![]() .
.
试题解析:解:(Ⅰ)由抛物线C:![]() 过点P(1,1),得
过点P(1,1),得![]() .
.
所以抛物线C的方程为![]() .
.
抛物线C的焦点坐标为(![]() ,0),准线方程为
,0),准线方程为![]() .
.
(Ⅱ)由题意,设直线l的方程为![]() (
(![]() ),l与抛物线C的交点为
),l与抛物线C的交点为![]() ,
,![]() .
.
由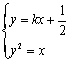 ,得
,得![]() .
.
则![]() ,
,![]() .
.
因为点P的坐标为(1,1),所以直线OP的方程为![]() ,点A的坐标为
,点A的坐标为![]() .
.
直线ON的方程为![]() ,点B的坐标为
,点B的坐标为![]() .
.
因为
![]()
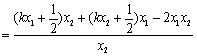
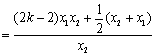
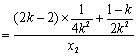
![]() ,
,
所以![]() .
.
故A为线段BM的中点.
【考点】1.抛物线方程;2.直线与抛物线的位置关系
【名师点睛】本题考查了直线与抛物线的位置关系,考查了转换与化归能力,当看到题目中出现直线与圆锥曲![]() 线时,不需要特殊技巧,只要联立直线与圆锥曲线的方程,借助根与系数关系,找准题设条件中突显的或隐含的等量关系,把这种关系“翻译”出来,有时不一定要把结果及时求出来,可能需要整
线时,不需要特殊技巧,只要联立直线与圆锥曲线的方程,借助根与系数关系,找准题设条件中突显的或隐含的等量关系,把这种关系“翻译”出来,有时不一定要把结果及时求出来,可能需要整
体代换到后面的计算中去,从而减少计算量.
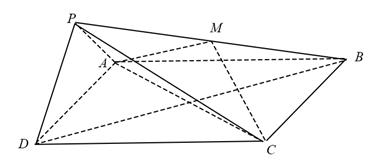
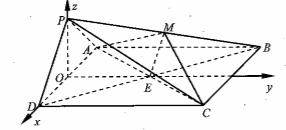
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
(Ⅰ)详见解析:(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】

试题解析:解:(I)设![]() 交点为
交点为![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点.
的中点.
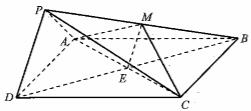
(II)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() .
.
如图建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则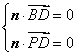 ,即
,即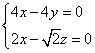 .
.
令![]() ,则
,则![]() ,
,![]() .于是
.于是![]() .
.
平面![]() 的法向量为
的法向量为![]() ,所以
,所以![]() .
.
由题知二面角![]() 为锐角,所以它的大小为
为锐角,所以它的大小为![]() .
.
(III)由题意知![]() ,
,![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【考点】1.线线,线面的位置关系;2.向量法.
【名师点睛】本题涉及到了立体几何中的线面平行与垂直的判定与性质,全面考查立体几何中的证明与求解,意在考查学生的空间想象能力和逻辑推理能力;利用空间向量解决立体几何问题是一种成熟的方法,要注意建立适当的空间直角坐标系以及运算的准确性.
已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)![]() ;(Ⅱ)最大值1;最小值
;(Ⅱ)最大值1;最小值![]() .
.
【解析】
试题分析:(Ⅰ)根据导数的几何意义,求斜率再代入切线方程公式![]() ;(Ⅱ)设
;(Ⅱ)设![]() ,求
,求![]() ,根据
,根据![]() 确定函数
确定函数![]() 的单调性,根据单调减求函数的最大值
的单调性,根据单调减求函数的最大值![]() ,可以知道
,可以知道![]() 恒成立,所以函数
恒成立,所以函数![]() 是单调递减函数,根据单调性求最值.
是单调递减函数,根据单调性求最值.
试题解析:(Ⅰ)因为![]() ,所以
,所以![]() .
.
又因为![]() ,所以曲线
,所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.

【考点】1.导数的几何意义;2.利用导数求函数的最值.
【名师点睛】这道导数题并不难,比一般意义上的压轴题要简单很多,第二问比较有特点是需要求二阶导数,因为![]() 不能判断函数的单调性,所以需要再求一次导数,设
不能判断函数的单调性,所以需要再求一次导数,设![]() ,再求
,再求![]() ,一般这时就可求得函数
,一般这时就可求得函数![]() 的零点,或是
的零点,或是![]() 恒成立,这样就能知道函数
恒成立,这样就能知道函数![]() 的单调性,根据单调性求最值,从而判断
的单调性,根据单调性求最值,从而判断![]() 的单调性,求得最值.
的单调性,求得最值.
为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者.
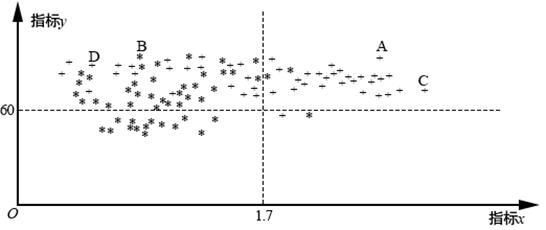
(Ⅰ)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;
(Ⅱ)从图中A,B,C,D四人中随机.选出两人,记![]() 为选出的两人中指标x的值大于1.7的人数,求
为选出的两人中指标x的值大于1.7的人数,求![]() 的分布列和数学期望E(
的分布列和数学期望E(![]() );
);
(Ⅲ)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
(Ⅰ)0.3;(Ⅱ)详见解析;(Ⅲ)在这100名患者中,服药者指标![]() 数据的方差大于未服药者指标
数据的方差大于未服药者指标![]() 数据的方差.
数据的方差.
【解析】

(Ⅱ)由图知,A,B,C,D四人中,指标![]() 的值大于1.7的有2人:A和C.
的值大于1.7的有2人:A和C.
所以![]() 的所有可能取值为0,1,2.
的所有可能取值为0,1,2.
![]() .
.
所以![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
|
|
|
|
|
故![]() 的期望
的期望![]() .
.
(Ⅲ)在这100名患者中,服药者指标![]() 数据的方差大于未服药者指标
数据的方差大于未服药者指标![]() 数据的方差.
数据的方差.
【考点】1.古典概型;2.超几何分布;3.方差的定义.
【名师点睛】求分布列的三种方法
1.由统计数据得到离散型随机变量的分布列;
2.由古典概型求出离散型随机变量的分布列;
3.由互斥事件的概率、相互独立事件同时发生的概率及n次独立重复试验有k次发生的概率求离散型随机变量的分布列.
本卷还有15题,登录并加入会员即可免费使用哦~

该作品由: 用户江河分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。