2017_2018学年高中数学第一章统计章末综合测评试卷及答案北师大版必修3
高中
整体难度：中等
2017-07-20
题号
一
二
三
四
五
评分
一、解答题 (共6题)
添加该题型下试题
1.
某城市100户居民的月平均用电量(单位：度)，以[160,180)，[180,200)，[200,220)，[220,240)，[240,260)，[260,280)，[280,300]分组的频率分布直方图如图6.
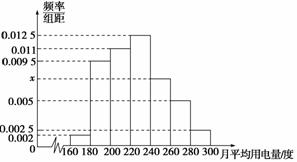
图6
(1)求直方图中x的值；
(2)求月平均用电量的众数和中位数；
(3)在月平均用电量为[220,240)，[240,260)，[260,280)，[280,300]的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220,240)的用户中应抽取多少户？
难度：
知识点：统计
使用次数：166
【答案】
【解】 (1)由(0.002＋0.009 5＋0.011＋0.012 5＋x＋0.005＋0.002 5)×20＝1得x＝0.007 5，
∴直方图中x的值为0.007 5.
(2)月平均用电量的众数是
＝230.
∵(0.002＋0.009 5＋0.011)×20＝0.45<0.5，
∴月平均用电量的中位数在[220,240)内，设中位数为a，则(0.002＋0.009 5＋0.011)×20＋0.012 5×(a－220)＝0.5，解得a＝224，即中位数为224.
(3)月平均用电量在[220,240)的用户有0.012 5×20×100＝25(户)，同理可求月平均用电量为[240,260)，[260,280)，[280,300]的用户分别有15户、10户、5户，故抽取比例为
＝
，
∴从月平均用电量在[220,240)的用户中应抽取25×＝5(户)．
2.
某市为了考核甲、乙两部门的工作情况，随机访问了50位市民．根据这50位市民对这两部门的评分(评分越高表明市民的评价越高)，绘制茎叶图如下：
| 甲部门 |
| 乙部门 |
|
| 3 | 5 9 |
| 4 | 4 | 0 4 4 8 |
| 9 7 | 5 | 1 2 2 4 5 6 6 7 7 7 8 9 |
| 9 7 6 6 5 3 3 2 1 1 0 | 6 | 0 1 1 2 3 4 6 8 8 |
| 9 8 8 7 7 7 6 6 5 5 5 5 5 4 4 4 3 3 3 2 1 0 0 | 7 | 0 0 1 1 3 4 4 9 |
| 6 6 5 5 2 0 0 | 8 | 1 2 3 3 4 5 |
| 6 3 2 2 2 0 | 9 | 0 1 1 4 5 6 |
|
| 10 | 0 0 0 |
图5
(1)分别估计该市的市民对甲、乙两部门评分的中位数；
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率；
(3)根据茎叶图分析该市的市民对甲、乙两部门的评价．
难度：
知识点：统计
使用次数：110
【答案】
【解】 (1)由所给茎叶图知，将50位市民对甲部门的评分由小到大排序，排在第25,26位的是75,75，故样本的中位数为75，所以该市的市民对甲部门评分的中位数的估计值是75.50位市民对乙部门的评分由小到大排序，排在第25,26位的是66,68，故样本中位数为
＝67，所以该市的市民对乙部门评分的中位数的估计值是67.
(2)由所给茎叶图知，50位市民对甲、乙部门的评分高于90的比率分别为
＝0.1，
＝0.16，故该市的市民对甲、乙部门的评分高于90的概率的估计值分别为0.1,0.16.
(3)由所给茎叶图知，市民对甲部门的评分的中位数高于对乙部门的评分的中位数，而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差，说明该市市民对甲部门的评价较高、评价较为一致，对乙部门的评价较低、评价差异较大．
3.
为了了解中学生的身体发育情况，对某一中学同年龄的50名男生的身高进行了测量，结果如下：[157,161)3人；[161,165)4人；[165,169)12人；[169,173)13人；[173,177)12人；[177,181]6人.
(1)列出频率分布表；
(2)画出频率分布直方图；
(3)估计总体在[165,177)间的比例．
难度：
知识点：统计
使用次数：198
【答案】
【解】 (1)列出频率分布表：
| 分组 | 频数 | 频率 |
|
| [157,161) | 3 | 0.06 | 0.015 |
| [161,165) | 4 | 0.08 | 0.02 |
| [165,169) | 12 | 0.24 | 0.06 |
| [169,173) | 13 | 0.26 | 0.065 |
| [173,177) | 12 | 0.24 | 0.06 |
| [177,181] | 6 | 0.12 | 0.03 |
| 合计 | 50 | 1.00 |
(2)画出频率分布直方图如图：
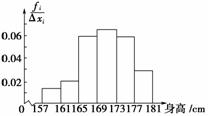
(3)因0.24＋0.26＋0.24＝0.74，
所以估计总体在[165,177)间的比例为74%.
4.
为了了解小学生的体能情况，抽取了某校一个年级的部分学生进行一分钟跳绳次数测试，将取得数据整理后，画出频率分布直方图(如图4)．已知图中从左到右前三个小组频率分别为0.1,0.3,0.4，第一小组的频数为5.
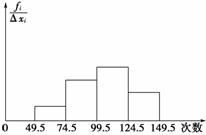
图4
(1)求第四小组的频率；
(2)参加这次测试的学生有多少人；
(3)若次数在75次以上(含75次)为达标，试估计该年级学生跳绳测试的达标率是多少．
难度：
知识点：统计
使用次数：188
【答案】
【解】 (1)由累积频率为1知，第四小组的频率为1－0.1－0.3－0.4＝0.2.
(2)设参加这次测试的学生有x人，则0.1x＝5，∴x＝50.
即参加这次测试的学生有50人．
(3)达标率为0.3＋0.4＋0.2＝0.9，∴估计该年级学生跳绳测试的达标率为90%.
5.
两台机床同时生产一种零件，在10天中，两台机床每天的次品数如下：
甲：1,0,2,0,2,3,0,4,1,2；
乙：1,3,2,1,0,2,1,1,0,1.
(1)哪台机床次品数的平均数较小？
(2)哪台机床的生产状况比较稳定？
难度：
知识点：统计
使用次数：132
【答案】
【解】 (1) 
甲＝(1＋0＋2＋0＋2＋3＋0＋4＋1＋2)×
＝1.5，乙＝(1＋3＋2＋1＋0＋2＋1＋1＋0＋1)×＝1.2.
∵甲＞乙，∴乙车床次品数的平均数较小．
(2)s
＝[(1－1.5)2＋(0－1.5)2＋(2－1.5)2＋(0－1.5)2＋(2－1.5)2＋(3－1.5)2＋(0－1.5)2＋(4－1.5)2＋(1－1.5)2＋(2－1.5)2]＝1.65，
同理s＝0.76，∵s＞s，∴乙车床的生产状况比较稳定．
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
中等
难度统计
难度系数
数量
占比
中等
6
27.27%
容易
16
72.72%
题型统计
大题类型
数量
占比
解答题
6
27.27%
填空题
4
18.18%
选择题
12
54.54%
知识点统计
知识点
数量
占比
统计
22
100.0%
版权提示
该作品由: 用户疯分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。