2017陕西高一下学期高中数学期中考试128615
高中
整体难度：中等
2017-10-18
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
已知集合M={x|﹣1＜x＜3}，N={x|x2+2x﹣3＜0}，则集合M∩N等于（ ）
A．{x|﹣1＜x＜3} B．{x|﹣3＜x＜1} C．{x|﹣1＜x＜1} D．{x|﹣3＜x＜3}
难度：
知识点：集合与函数的概念
使用次数：194
【答案】
C
【考点】1E：交集及其运算．
【分析】先求出集合N，由此能求出M∩N．
【解答】解：∵集合M={x|﹣1＜x＜3}，
N={x|x2+2x﹣3＜0}={x|﹣3＜x＜1}，
∴集合M∩N={x|﹣1＜x＜1}．
故选：C．
2.
如图所示，在三棱台A′B′C′﹣ABC中，沿A′BC截去三棱锥A′﹣ABC，则剩余的部分是（ ）
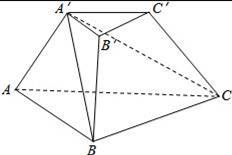
A．三棱锥 B．四棱锥 C．三棱柱 D．组合体
难度：
知识点：空间几何体
使用次数：133
【答案】
B【考点】L1：构成空间几何体的基本元素．
【分析】画出图形，根据图形和四棱锥的结构特征，即可得出剩余几何体是什么图形．
【解答】解：如图所示，
三棱台A′B′C′﹣ABC中，沿A′BC截去三棱锥A′﹣ABC，
剩余部分是四棱锥A′﹣BCC′B′．
故选：B．
3.
在△ABC中，
，
，
，则C=（ ）
A．
B．
C．
D．
难度：
知识点：解三角形
使用次数：113
【答案】
D【考点】HP：正弦定理．
【分析】运用三角形的内角和定理可得角A，再由正弦定理，计算即可得到C．
【解答】解：由A=60°，
＞，
则A＞B．
由正弦定理
=
，
则有
，
得：sinB=
，
∵A＞B，
∴B=．
则C=
，
故选：D．
4.
在等比数列{an}中，a1=﹣16，a4=8，则a7=（ ）
A．﹣4 B．±4 C．﹣2 D．±2
难度：
知识点：数列
使用次数：163
【答案】
A【考点】88：等比数列的通项公式．
【分析】由等比数列的性质可得，a1•a7=a42结合已知可求
【解答】解：由等比数列的性质可得，a1•a7=a42
5.
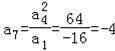
若a，b，c为实数，则下列命题错误的是（ ）
A．若ac2＞bc2，则a＞b B．若a＜b＜0，则a2＜b2
C．若a＞b＞0，则
＜
D．若a＜b＜0，c＞d＞0，则ac＜bd
难度：
知识点：不等式
使用次数：173
【答案】
B【考点】R3：不等式的基本性质．
【分析】根据不等式的基本性质，判断每个选项即可
【解答】解：对于A：若ac2＞bc2，则a＞b，故正确，
对于B：根据不等式的性质，若a＜b＜0，则a2＞b2，故B错误，
对于C：若a＞b＞0，则
＞
，即
＞
，故正确，
对于D：若a＜b＜0，c＞d＞0，则ac＜bd，故正确．
本卷还有16题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
21
总体难度：
中等
难度统计
难度系数
数量
占比
容易
9
42.85%
中等
12
57.14%
题型统计
大题类型
数量
占比
选择题
12
57.14%
填空题
4
19.04%
计算题
1
4.76%
解答题
4
19.04%
知识点统计
知识点
数量
占比
集合与函数的概念
2
9.52%
空间几何体
4
19.04%
解三角形
3
14.28%
数列
5
23.80%
不等式
5
23.80%
基本初等函数I
1
4.76%
几何证明选讲
1
4.76%
版权提示
该作品由: 用户yh3109分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。