2019湖北高中数学月考试卷135114
高中
整体难度：中等
2019-08-17
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
若直线
过第一、三、四象限，则实数
满足（ ）
A. 
B. 
C. 
D. 
难度：
知识点：直线与方程
使用次数：148
【答案】
C
【解析】
【分析】
根据题意画出图形，结合图形知a＞0且b＞0．
【详解】直线
过第一、三、四象限，如图所示；
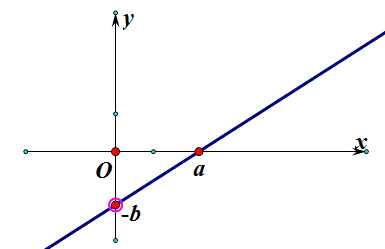
则a＞0，-b＜0．
即a＞0且b＞0．
故选：C．
【点睛】本题考查了直线方程的应用问题，是基础题．
2.
用辗转相除法计算60和48的最大公约数时，需要做的除法次数是（ ）
A. 1 B. 2 C. 3 D. 4
难度：
知识点：算法初步
使用次数：153
【答案】
B
【解析】
【分析】
直接利用辗转相除法的原理求需要做的除法次数.
【详解】解：∵60=1×48+12,
48=4×12 ,
60和48的最大公约数是12 .
所以需要做的除法次数2 .
故选：B
【点睛】本题主要考查辗转相除法，意在考查学生对该知识的理解掌握水平和分析推理能力.
3.
过原点且倾斜角为
的直线被圆
所截得的弦长为（ ）
A. 
B. 
C. 
D. 
难度：
知识点：圆与方程
使用次数：117
【答案】
D
【解析】
【分析】
列出直线方程，运用点到直线的距离公式求得圆心到直线的距离，进而求弦长.
【详解】过原点且倾斜角为30°的直线方程为
，圆x2+（y-2）2=4的圆心为（0，2），半径r=2，
圆心到直线的距离为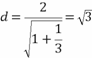
，则截得的弦长为
故选：D
【点睛】本题考查直线和圆相交的弦长问题，圆的弦长问题首选几何法，即利用圆的半径、弦心距、弦长的一半满足勾股定理求解.
4.
若
，则
等于（ ）
A. 
B. 
C. 
D. 
难度：
知识点：三角函数
使用次数：187
【答案】
B
【解析】
试题分析：
，
.
考点：三角恒等变形、诱导公式、二倍角公式、同角三角函数关系．
5.
交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为
，其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43，则这四个社区驾驶员的总人数为（ ）
A. 101 B. 808 C. 1212 D. 2012
难度：
知识点：统计
使用次数：161
【答案】
B
【解析】
试题分析：由分层抽样的定义可得
，解得
，答案选B．
考点：分层抽样
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
中等
难度统计
难度系数
数量
占比
容易
12
54.54%
中等
9
40.90%
偏难
1
4.54%
题型统计
大题类型
数量
占比
选择题
12
54.54%
填空题
4
18.18%
解答题
5
22.72%
综合题
1
4.54%
知识点统计
知识点
数量
占比
直线与方程
4
18.18%
算法初步
2
9.09%
圆与方程
5
22.72%
三角函数
2
9.09%
统计
4
18.18%
概率
1
4.54%
球面上的几何
1
4.54%
不等式
1
4.54%
数列
1
4.54%
点 直线 平面之间的位置
1
4.54%
版权提示
该作品由: 用户njzx分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。