.设![]() 是虚数单位,则
是虚数单位,则![]() (
(
A. i B. ![]() C.
C. ![]() D. 0
D. 0
D
【解析】
【分析】
把复数z代入,然后直接利用复数代数形式的除法运算化简求值
【详解】解:![]() 是虚数单位,则
是虚数单位,则![]() ,
,
故选:D.
【点睛】本题考查了复数代数形式的除法运算,是基础的计算题.
以下判断正确的是( )
A. 函数![]() 为
为![]() 上可导函数,则
上可导函数,则![]() 是
是![]() 为函数
为函数![]() 极值点的充要条件
极值点的充要条件
B. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
C. “![]() ”是“函数
”是“函数![]() 是偶函数”的充要条件
是偶函数”的充要条件
D. 命题“在![]() 中,若
中,若![]() ,则
,则![]() ”的逆命题为假命题
”的逆命题为假命题
C
【解析】
对于![]() ,函数
,函数![]() 为
为![]() 上可导函数,则
上可导函数,则![]() 是
是![]() 为函数
为函数![]() 极值点的必要不充分条件,如
极值点的必要不充分条件,如![]() ,满足
,满足![]() ,但
,但![]() 不是函数的极值点,故
不是函数的极值点,故![]() 错误;对于
错误;对于![]() ,命题“
,命题“![]() ”的否定是“
”的否定是“![]() ”,故
”,故![]() 错误;对于
错误;对于![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,函数为偶函数,反之,若函数
,函数为偶函数,反之,若函数![]() 是偶函数,则
是偶函数,则![]() ,即
,即![]() ,“
,“![]() ”, 是“函数
”, 是“函数![]() 是偶函数”,的充要条件,故
是偶函数”,的充要条件,故![]() 正确;对于
正确;对于![]() ,在
,在![]() 中,若“
中,若“![]() ,则
,则![]() ,” 的逆命题为“若
,” 的逆命题为“若![]() ,则
,则![]() ”,由正弦定理可知,在
”,由正弦定理可知,在![]() 中,
中,![]() ,逆命题为真命题,故
,逆命题为真命题,故![]() 错误,故选C.
错误,故选C.
下列函数中,在![]() 上单调递增,并且是偶函数的是( )
上单调递增,并且是偶函数的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
C
【解析】
试题分析:四个函数中,是偶函数的有![]() ,又
,又![]() 在
在![]() 内单调递增,故选C.
内单调递增,故选C.
考点:函数的单调性与奇偶性.
已知函数![]() ,
,![]() ,
,![]() 的零点分别为a,b,c,则a,b,c的大小关系为
的零点分别为a,b,c,则a,b,c的大小关系为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
A
【解析】
∵函数![]() ,
,![]() ,
,![]() 的零点分别为
的零点分别为![]()
∴![]() ,
,![]() ,
,![]()
即![]() ,
,![]() ,
,![]()
∴根据函数图象可得,![]() ,
,![]() ,
,![]()
∴![]()
故选A
在同一坐标系内,函数![]() 和
和![]() 的图象可能是( )
的图象可能是( )
A. 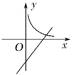 B.
B. 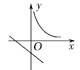 C.
C. 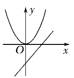 D.
D. 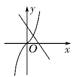
B
【解析】
【分析】
分两种情况讨论,利用函数的单调性,筛选排除即可得结果
【详解】若![]()
![]() 在
在![]() 递增,排除
递增,排除![]() 选项,
选项,
![]() 递增,排除
递增,排除![]() ;纵轴上截距为正数,排除
;纵轴上截距为正数,排除![]() ,
,
即![]() 时,不合题意;
时,不合题意;
若![]() ,
,![]() 在
在![]() 递减,可排除
递减,可排除![]() 选项,
选项,
由![]() 递减可排除
递减可排除![]() ,故选B.
,故选B.
【点睛】本题通过对多个图象的选择考查函数的图象与性质,属于中档题.这类题型也是近年高考常见的命题方向,该题型的特点是综合性较强、考查知识点较多,但是并不是无路可循.解答这类题型可以从多方面入手,根据函数的定义域、值域、单调性、奇偶性、特殊点以及![]() 时函数图象的变化趋势,利用排除法,将不合题意的选项一一排除.
时函数图象的变化趋势,利用排除法,将不合题意的选项一一排除.
本卷还有18题,登录并加入会员即可免费使用哦~

该作品由: 用户毛毛分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。