2020宁夏高二上学期人教A版(2019)高中数学期中考试135793
高中
整体难度：中等
2019-11-26
题号
一
二
三
四
五
评分
一、解答题 (共6题)
添加该题型下试题
1.
在平面直角坐标系中,记满足
的点
形成区域
.
(1)若点的横、纵坐标均在集合
中随机选择，求点落在区域内的概率
(2)点落在区域内均匀出现，求方程
有两个不相等实数根的概率
难度：
知识点：概率
使用次数：147
【答案】
试题解析：（1）根据题意，点（p，q），在|p|≤3，|q|≤3中，即如图所在正方形区域，
其中p、q都是整数的点有6×6=36个，
点M（x，y）横、纵坐标分别由掷骰子确定，即x、y都是整数，且1≤x≤3，1≤y≤3，
点M（x，y）落在上述区域有（1，1），（1，2），（1，3），
（2，1），（2，2），（2，3），（3，1），（3，2），（3，3），有9个点，
所以点M（x，y）落在上述区域的概率
（2）|p|≤3，|q|≤3表示如图的正方形区域，易得其面积为36；
若方程有两个实数根，则有△=4-4q>0，
解可得q<1，表示q=1下方的部分，其面积为24，
即方程有两个实数根的概率，
2.
已知命题
：方程
表示焦点在
轴上的椭圆，命题
：
,不等式
恒成立.
（1）若“
”是真命题，求实数
的取值范围；
（2）若“
”为假命题，“
”为真命题，求实数的取值范围.
难度：
知识点：常用逻辑用语
使用次数：155
【答案】
解：（Ⅰ）因为对任意实数
不等式恒成立，
所以
，解得
，．…………2分
又“
”是真命题等价于“”是假命题，．…………3分
所以所求实数的取值范围是
．…………4分
（Ⅱ）
，……6分
，………7分
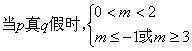，无解…………9分
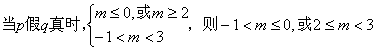，…………11分
．…………12分
3.
某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每种单价（x元）试销
天，得到如表单价x（元）与销量y（册）数据：
| 单价x（元） | 18 | 19 | 20 | 21 | 22 |
| 销量y（册） | 61 | 56 | 50 | 48 | 45 |
(1)根据表中数据，请建立
关于的回归直线方程：
(2)预计今后的销售中，销量（册）与单价（元）服从（l）中的回归方程，已知每册书的成本是12元，书店为了获得最大利润，该册书的单价应定为多少元？
附：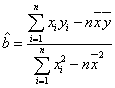
，
，
，
难度：
知识点：统计
使用次数：194
【答案】
解：（1）
，
，
，
所以对的回归直线方程为：
．
（2）设获得的利润为
，
，
因为二次函数
的开口向下，
所以当
时，取最大值，
所以当单价应定为22.5元时，可获得最大利润．
4.
年年底，某城市地铁交通建设项目已经基本完成，为了解市民对该项目的满意度，分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
分)，绘制如下频率分布直方图，并将分数从低到高分为四个等级：
| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有
人．
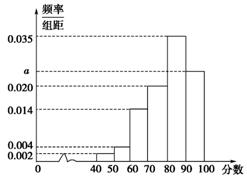
(1)求频率分布于直方图中
的值，及评分等级不满意的人数；
(2)相关部门对项目进行验收，验收的硬性指标是：市民对该项目的满意指数不低于
，否则该项目需进行整改，根据你所学的统计知识，判断该项目能否通过验收，并说明理由.
难度：
知识点：统计
使用次数：113
【答案】
（1）由频率分布直方图知，
由
解得
，
设总共调查了
个人，则基本满意的为
，解得
人.
不满意的频率为
，所以共有
人，即不满意的人数为120人.
.（2）所选样本满意程度的平均得分为：
，
估计市民满意程度的平均得分为
，
所以市民满意指数为
，
故该项目能通过验收.
5.
抛物线
的焦点为
，斜率为正的直线
过点交抛物线于、
两点，满足
．
(1)求直线的斜率；
(2)过焦点与垂直的直线交抛物线于
两点，求四边形
的面积．
难度：
知识点：圆锥曲线与方程
使用次数：184
【答案】
（1）依题意知F（1,0），设直线AB的方程为
．将直线AB的方程与抛物线的方程联立，消去x得
．设
， 
，所以
， 
．①因为
，所以
．②联立①和②，消去
，得．
与又
所以直线AB的斜率是
．
(2)
直线
的斜率
直线CD的方程
，将直线CD的方程与抛物线的方程联立,消去
得：
设
由（1）知 
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
中等
难度统计
难度系数
数量
占比
中等
11
50.0%
容易
11
50.0%
题型统计
大题类型
数量
占比
解答题
6
27.27%
填空题
4
18.18%
选择题
12
54.54%
知识点统计
知识点
数量
占比
概率
2
9.09%
圆锥曲线与方程
9
40.90%
统计
6
27.27%
推理与证明
1
4.54%
算法初步
1
4.54%
常用逻辑用语
3
13.63%
版权提示
该作品由: 用户刘奕君分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。