2020河北高三上学期高中数学开学考试136966
高中
整体难度：中等
2020-04-17
题号
一
二
三
四
五
评分
一、选择题 (共11题)
添加该题型下试题
1.
设函数
的定义域
，函数
的定义域为
，则
（）
A. 
B. 
C. 
D. 
难度：
知识点：基本初等函数I
使用次数：117
【答案】
C
【解析】
【分析】
根据幂函数及对数函数定义域的求法，即可求得和，即可求得
．
【详解】解：由
，解得：
，则函数的定义域
，
由对数函数的定义域可知：
，解得：
，则函数的定义域
，
则，
故选C．
【点睛】本题考查函数定义的求法，交集及其运算，考查计算能力，属于基础题．
2.
设
，则
A. 
B. 
C. 
D. 
难度：
知识点：数系的扩充与复数的引入
使用次数：112
【答案】
C
【解析】
分析：利用复数的除法运算法则：分子、分母同乘以分母的共轭复数，化简复数
，然后求解复数的模.
详解：
，
则
，故选c.
点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.
3.
若f(x)=ln(x2-2ax+1+a)在区间
上递减,则实数
的取值范围为（ ）
A. 
B. 
C. 
D. 
难度：
知识点：基本初等函数I
使用次数：110
【答案】
B
【解析】
【分析】
由外函数对数函数是增函数，可得要使函数
在上递减，需内函数二次函数的对称轴大于等于1，且内函数在上的最小值大于0，由此联立不等式组求解．
【详解】解：令
，其对称轴方程为
，
外函数对数函数是增函数，
要使函数在上递减，
则
，即：
．
实数的取值范围是
．
故选：．
【点睛】本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．
4.
《九章算术》中的“两鼠穿墙”问题为“今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，问何日相逢？”可用如图所示的程序框图解决此类问题.现执行该程序框图，输入的
的值为33，则输出的
的值为
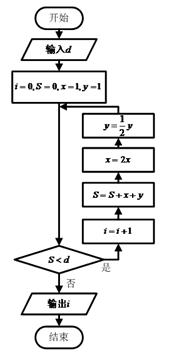
A. 4 B. 5 C. 6 D. 7
难度：
知识点：算法初步
使用次数：186
【答案】
C
【解析】
【详解】
，开始执行程序框图，
，，
，
退出循环，输出
，故选C.
5.
已知定义域为
的奇函数
满足
，且当
时，
，则
（）
A. 
B. 
C. 3 D. 
难度：
知识点：集合与函数的概念
使用次数：109
【答案】
D
【解析】
【分析】
由题意利用函数奇偶性求得的周期为3，再利用函数的周期性求得
的值．
【详解】解：
已知定义域为的奇函数满足，
，的周期为3.
时，，
,
故选D．
【点睛】本题主要考查函数奇偶性和周期性，函数值的求法，属于基础题．
本卷还有18题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
23
总体难度：
中等
难度统计
难度系数
数量
占比
中等
14
60.86%
容易
9
39.13%
题型统计
大题类型
数量
占比
选择题
11
47.82%
解答题
8
34.78%
填空题
4
17.39%
知识点统计
知识点
数量
占比
基本初等函数I
3
13.04%
数系的扩充与复数的引入
1
4.34%
算法初步
1
4.34%
集合与函数的概念
2
8.69%
概率
1
4.34%
平面向量
2
8.69%
计数原理
1
4.34%
数列
2
8.69%
圆锥曲线与方程
1
4.34%
球面上的几何
1
4.34%
导数及其应用
1
4.34%
不等式
2
8.69%
统计
2
8.69%
解三角形
1
4.34%
点 直线 平面之间的位置
1
4.34%
坐标系与参数方程
1
4.34%
版权提示
该作品由: 用户阿曾分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。