2020浙江高中数学高考真题137205
高中
整体难度：中等
2020-07-11
题号
一
二
三
四
五
评分
一、解答题 (共4题)
添加该题型下试题
1.
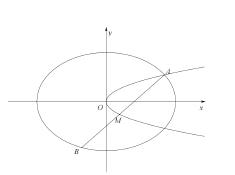
如图，已知椭圆
，抛物线
，点A是椭圆
与抛物线
的交点，过点A的直线l交椭圆于点B，交抛物线于M（B，M不同于A）．
（Ⅰ）若
，求抛物线的焦点坐标；
（Ⅱ）若存在不过原点的直线l使M为线段AB的中点，求p的最大值．
难度：
知识点：高考试题
使用次数：131
【答案】
（Ⅰ）
；（Ⅱ）
【解析】
【分析】
（Ⅰ）将p代入方程求得抛物线方程即可得到焦点坐标；
（Ⅱ）设
，联立直线与椭圆方程得到根与系数的关系，进一步得到M的坐标，进一步得到关于
的方程，联立直线与抛物线方程得到
，再联立抛物线与椭圆方程得到
，即可建立方程，再利用基本不等式求最值即可.
【详解】（Ⅰ）当时，的方程为
，故抛物线的焦点坐标为；
（Ⅱ）设
由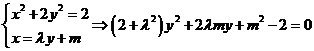
由M在抛物线上，所以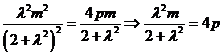
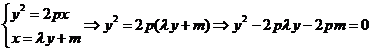
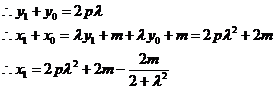
由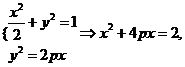
即
所以
，
，
，
所以，
的最大值为，此时
.
【点晴】本题主要考查直线与圆锥曲线的位置关系的综合应用，涉及到求函数的最值，考查学生的数学运算能力，是一道有一定难度的题.
2.
在锐角△ABC中，角A，B，C的对边分别为a，b，c，且
．
（I）求角B；
（II）求cosA+cosB+cosC的取值范围．
难度：
知识点：高考试题
使用次数：114
【答案】
（I）
；（II）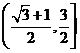
【解析】
【分析】
（I）首先利用正弦定理边化角，然后结合特殊角的三角函数值即可确定∠B的大小；
（II）结合(1)的结论将含有三个角的三角函数式化简为只含有∠A的三角函数式，然后由三角形为锐角三角形确定∠A的取值范围，最后结合三角函数的性质即可求得
的取值范围.
【详解】（I）由结合正弦定理可得：
△ABC为锐角三角形，故.
（II）结合(1)的结论有：
.
由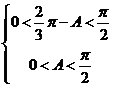
可得：
，
，
则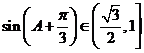
，
.
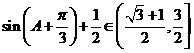即的取值范围是.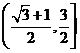
【点睛】解三角形的基本策略：一是利用正弦定理实现“边化角”，二是利用余弦定理实现“角化边”；求最值也是一种常见类型，主要方法有两类，一是找到边之间的关系，利用基本不等式求最值，二是转化为关于某个角的函数，利用函数思想求最值.
3.
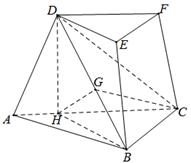
如图，三棱台DEF—ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC =2BC．
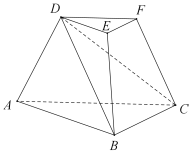
（I）证明：EF⊥DB；
（II）求DF与面DBC所成角的正弦值．
难度：
知识点：高考试题
使用次数：159
【答案】
（I）证明见解析；（II）
【解析】
【分析】
（I）作
交
于
，连接
，由题意可知
平面
，即有
，根据勾股定理可证得
，又
，可得
，
，即得
平面
，即证得
；
（II）由
，所以
与平面
所成角即为
与平面所成角，作
于
，连接
，即可知
即为所求角，再解三角形即可求出与平面所成角的正弦值．
详解】（I）作交于，连接．
∵平面
平面，而平面
平面
，
∴平面，即有．
∵
，
∴
．
在
中，
，即有
，∴
．
由棱台的定义可知，，所以，，而
，
∴平面，而
平面，∴．
（II）因为，所以与平面所成角即为与平面所成角．
作于，连接，由（1）可知，
平面，所以平面
平面，而平面
平面
，∴
平面
．
即在平面内的射影为，即为所求角．
在
中，设
，则
，
，
∴
．
故与平面所成角的正弦值为．
【点睛】本题主要考查空间点、线、面位置关系，线面垂直的判定定理的应用，直线与平面所成的角的求法，意在考查学生的直观想象能力和数学运算能力，属于基础题．
4.
已知数列{an}，{bn}，{cn}中，
．
（Ⅰ）若数列{bn}为等比数列，且公比
，且
，求q与an的通项公式；
（Ⅱ）若数列{bn}为等差数列，且公差
，证明：
．
难度：
知识点：高考试题
使用次数：127
【答案】
（I）
；（II）证明见解析
【解析】
【分析】
（I）根据，求得
，进而求得数列
的通项公式，利用累加法求得数列
的通项公式.
（II）利用累乘法求得数列的表达式，结合裂项求和法证得不等式成立.
【详解】（I）依题意
，而，即
，由于，所以解得
，所以
.
所以
，故
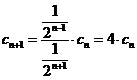，所以数列是首项为
，公比为
的等比数列，所以
.所以
.
所以
，故
（
）.
所以
.
（II）依题意设
，由于
，
所以
，
故
.
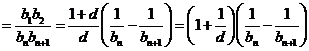所以
.
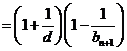由于
，所以
，所以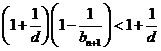
.
即
.
【点睛】本小题主要考查累加法、累乘法求数列的通项公式，考查裂项求和法，属于中档题.
二、综合题 (共1题)
添加该题型下试题
1.
已知
，函数
，其中e=2.71828…为自然对数的底数．
（Ⅰ）证明：函数
在
上有唯一零点；
（Ⅱ）记x0为函数在上的零点，证明：
（ⅰ）
；
（ⅱ）
．
难度：
知识点：高考试题
使用次数：142
【答案】
三、选择题 (共10题)
添加该题型下试题
本卷还有17题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
22
总体难度：
中等
难度统计
难度系数
数量
占比
中等
8
36.36%
偏难
1
4.54%
基础
5
22.72%
容易
8
36.36%
题型统计
大题类型
数量
占比
解答题
4
18.18%
综合题
1
4.54%
选择题
10
45.45%
填空题
7
31.81%
知识点统计
知识点
数量
占比
高考试题
22
100.0%
版权提示
该作品由: 用户红天分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。