2019天津高二下学期人教A版(2019)高中数学期中考试137406
高中
整体难度：中等
2020-08-18
题号
一
二
三
四
五
评分
一、解答题 (共3题)
添加该题型下试题
2.
已知函数
.
（1）判断函数
的单调性；
（2）当在
上的最小值是
时，求m的值.
难度：
知识点：导数及其应用
使用次数：142
【答案】
(1)见解析；(2) 
【解析】
【点睛】本题考查了利用导数求函数的单调性，也考查了利用函数在区间上的最小值求参数的问题，属于中档题.
3.
已知函数
．若函数
在
处有极值-4．
（1）求的单调递减区间；
（2）求函数在
上的最大值和最小值．
难度：
知识点：导数及其应用
使用次数：120
【答案】
（1）
；（2）
.
【解析】
先求出导函数，根据导数的几何意义得到关于
的方程组，求得后再根据导函数的符号求出单调递减区间．
由求出函数的单调区间，可以数判断函数在
上的单调性，求出函数在上的极值和端点值，通过比较可得的最大值和最小值．
试题解析：
（1）∵
，
∴
，
依题意有即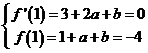
，解得
∴
，
由
，得
，
∴函数
单调递减区间
由知
∴
，
令
，解得
．
当
变化时，
的变化情况如下表：
由上表知，函数在
上单调递减，在
上单调递增．
故可得
又
．
∴
综上可得函数在上的最大值和最小值分别为
和
．
二、填空题 (共7题)
添加该题型下试题
1.
某单位安排
位员工在春节期间大年初一到初七值班，每人值班天，若位员工中的甲、乙排在相邻的两天，丙不排在初一，丁不排在初七，则不同的安排方案共有_______
难度：
知识点：计数原理
使用次数：146
【答案】
1008
【解析】
分析：本题的要求比较多，有三个限制条件，甲、乙排在相邻两天可以把甲和乙看做一个元素，注意两元之间有一个排列，丙不排在初一，丁不排在初七，则可以甲乙排初一、初二和初六、初七，丙排初七和不排初七，根据分类原理得到结果.
详解：分两类：
第一类：甲乙相邻排初一、初二或初六、初七，这时先安排甲和乙，有
种，然后排丙或丁，有
种，剩下的四人全排有
种，因此共有
种方法；
第二类：甲乙相邻排中间，有
种，当丙排在初七，则剩下的四人有
种排法，若丙排在中间，则甲有
种，初七就从剩下的三人中选一个，有
种，剩下三人有
种，所以共有
种，
故共有
种安排方案，故答案为
.
点睛：该题考查的是由多个限制条件的排列问题，在解题的过程中，注意相邻问题捆绑法，特殊元素优先考虑的原则，利用分类加法计数原理求得结果.
2.
设定义域为
的函数满足
，则不等式
的解集为__________．
难度：
知识点：导数及其应用
使用次数：144
【答案】
【解析】
【点睛】本题主要考查函数单调性的判断和应用，根据条件构造函数是解决本题的关键．
本卷还有14题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
19
总体难度：
中等
难度统计
难度系数
数量
占比
中等
1
5.26%
容易
18
94.73%
题型统计
大题类型
数量
占比
解答题
3
15.78%
填空题
7
36.84%
选择题
9
47.36%
知识点统计
知识点
数量
占比
导数及其应用
10
52.63%
计数原理
6
31.57%
数系的扩充与复数的引入
2
10.52%
基本初等函数I
1
5.26%
版权提示
该作品由: 用户张弓分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。