已知函数![]() ,其中
,其中![]() .
.
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:(1)因为![]() ,所以
,所以![]() .
.
所以![]() .
.
当![]() 时,由
时,由![]() 得
得![]() ;由
;由![]() 得
得![]() .故
.故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,由
时,由![]() 得
得![]() ;由
;由![]() 得
得![]() .故
.故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
综上可知,当![]() 时
时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时
时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)若![]() ,不等式转化为当
,不等式转化为当![]() 时,
时,![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
①当![]() 时,对任意
时,对任意![]() ,恒有
,恒有![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() 不合题意.
不合题意.
②当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,所以
,所以![]() 符合题意
符合题意
③当![]() 时,令
时,令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() .所以
.所以![]() 在
在![]() 上单调递增.所以
上单调递增.所以![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() ,
,
故![]() 不合题意.
不合题意.
综合①②③可知,实数![]() 的取值范围是
的取值范围是![]() .
.
2019年10月,工信部颁发了国内首个![]() 无线电通信设备进网许可证,标志着
无线电通信设备进网许可证,标志着![]() 基站设备将正式接入公用电信商用网络.某
基站设备将正式接入公用电信商用网络.某![]() 手机生产商拟升级设备生产
手机生产商拟升级设备生产![]() 手机,有两种方案可供选择,方案1:直接引进
手机,有两种方案可供选择,方案1:直接引进![]() 手机生产设备;方案2:对已有的
手机生产设备;方案2:对已有的![]() 手机生产设备进行技术改造,升级到
手机生产设备进行技术改造,升级到![]() 手机生产设备.该生产商对未来
手机生产设备.该生产商对未来![]() 手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
| 市场销售状态 | 畅销 | 平销 | 滞销 | |
| 市场销售状态概率 |
|
|
| |
| 预期年利润数值(单位:亿元) | 方案1 | 70 | 40 | -40 |
| 方案2 | 60 | 30 | -10 | |
(1)以预期年利润的期望值为依据,就![]() 的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
(2)设该生产商升级设备后生产的![]() 手机年产量为
手机年产量为![]() 万部,通过大数据模拟核算,选择方案1所生产的
万部,通过大数据模拟核算,选择方案1所生产的![]() 手机年度总成本
手机年度总成本![]() (亿元),选择方案2所生产的
(亿元),选择方案2所生产的![]() 手机年度总成本为
手机年度总成本为![]() (亿元).已知
(亿元).已知![]() ,当所生产的
,当所生产的![]() 手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,
手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,![]() (万元),
(万元),![]() (万元),根据(1)的决策,假设生产的手机全部售尽,求该生产商所生产的
(万元),根据(1)的决策,假设生产的手机全部售尽,求该生产商所生产的![]() 手机年利润期望的最大值?并判断这个最大值能否超过预期年利润的数值.
手机年利润期望的最大值?并判断这个最大值能否超过预期年利润的数值.
(1)由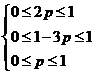 ,可得
,可得![]() 的取值范围为
的取值范围为![]() .
.
方案1的预期年利润期望值为
![]() .
.
方案2的预期年利润期望值为
![]() .
.
当![]() 时,
时,![]() ,该手机生产商应该选择方案1;
,该手机生产商应该选择方案1;
当![]() 时,
时,![]() ,该手机生产商可以选择方案1,也可以以选择方案2;
,该手机生产商可以选择方案1,也可以以选择方案2;
当![]() 时,
时,![]() ,该手机生产商应该选择方案2;
,该手机生产商应该选择方案2;
(2)因为![]() ,该手机生产商将选择方案1,此时生产的
,该手机生产商将选择方案1,此时生产的![]() 手机的年度总成本为
手机的年度总成本为![]() (亿元).
(亿元).
市场行情为畅销、平销和滞销时的年销售额分别为![]() ,
,![]() ,
,![]() (亿元),因为
(亿元),因为![]() ,所以手机生产商年销售额
,所以手机生产商年销售额![]() 的分布列为
的分布列为
|
|
|
|
|
|
| 0.4 | 0.4 | 0.2 |
所以![]()
![]() .
.
年利润期望值![]() (亿元).
(亿元).
当![]() 时,年利润期望
时,年利润期望![]() 取得最大值40亿元.
取得最大值40亿元.
又方案1的预期年利润期望值为![]()
![]() (亿元).
(亿元).
因为![]() ,因此这个年利润期望的最大值超过了预期年利润的数值.
,因此这个年利润期望的最大值超过了预期年利润的数值.
![]() 为虚数单位,
为虚数单位,![]() 是虚数,
是虚数, ![]() 是实数,且
是实数,且![]() ,
,![]() .
.
(1)求![]() 及
及![]() 的取值范围;
的取值范围;
(2)求![]() 的最小值.
的最小值.
解:(1)![]() ,因为
,因为![]() 是实数,
是实数,
所以![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() .
.
(2)由题意知![]() ,
,
所以![]()
![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以![]() 的最小值为1
的最小值为1
已![]() 知函数
知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)求![]() 和
和![]() 的值以及函数
的值以及函数![]() 的极大值和极小值;
的极大值和极小值;
(2)过点![]() 作曲线
作曲线![]() 的切线,求此切线的方程.
的切线,求此切线的方程.
解:(1)![]() ,由题意可知
,由题意可知![]() 是方程
是方程![]() 的两根,可得
的两根,可得![]() ,
,
所以![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() 在
在![]() 处取得极大值2,在
处取得极大值2,在![]() 处取得极小值-2;
处取得极小值-2;
(2)易知点![]() 不在曲线
不在曲线![]() 上,设切点坐标为
上,设切点坐标为![]() ,则有
,则有
![]() ,解得
,解得![]() ,
,
所以切线的斜率为9,切线的方程为![]()
某单位组织开展“学习强国”的学习活动,活动第一周甲、乙两个部门员工的学习情况统计如下:
| 学习活跃的员工人数 | 学习不活跃的员工人数 | |
| 甲 | 18 | 12 |
| 乙 | 32 | 8 |
(1)根据表中数据判断能否有95%的把握认为员工学习是否活跃与部门有关;
(2)活动第二周,单位为检查学习情况,从乙部门随机抽取2人,发现这两人学习都不活跃,能否认为乙部门第二周学习的活跃率比第一周降低了?说明理由。
参考公式:![]() ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
解:(1)![]() ,
,
因为![]() ,所以没有95%的把握认为员工学习是否活跃与部门有关;
,所以没有95%的把握认为员工学习是否活跃与部门有关;
(2)设事件![]() 为“第二周从乙部门随机抽取2人,这两人学习都不活跃”,若第二周保持第一周的活跃情况,则
为“第二周从乙部门随机抽取2人,这两人学习都不活跃”,若第二周保持第一周的活跃情况,则![]() ,
,
因为![]() 很小,所以事件
很小,所以事件![]() 一般不容易发生,现在发生了,则说明学习不活跃的人数增加了,即活跃率降低了.
一般不容易发生,现在发生了,则说明学习不活跃的人数增加了,即活跃率降低了.
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户可口可乐分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。