已知等差数列![]() 和等比数列
和等比数列![]() 的各项均为整数,它们的前
的各项均为整数,它们的前![]() 项和分别为
项和分别为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)求![]()
(3)是否存在正整数![]() ,使得
,使得![]() 恰好是数列
恰好是数列![]() 或
或![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)设数列![]() 的公差为
的公差为![]() ,数列
,数列![]() 的公比为
的公比为![]() ,
,
因为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() ,或
,或![]() (舍去).
(舍去).
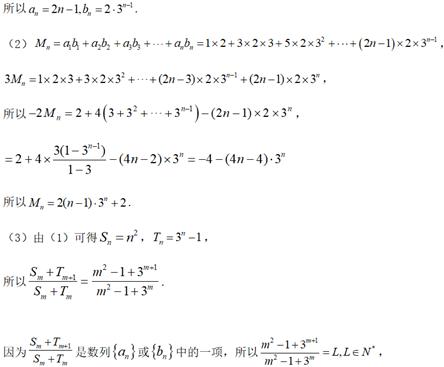

大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x和销售量y之间的一组数据如表所示:
| 月份i | 7 | 8 | 9 | 10 | 11 | 12 |
| 销售单价xi(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi(件) | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中![]() ,参考数据:
,参考数据:![]() .
.


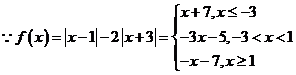 .
.
(1)当![]() 时,由
时,由![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
当![]() 时,由
时,由![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
当![]() 时,由
时,由![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上所述,不等式![]() 的解集
的解集![]() ;
;
(2)当![]() 时,函数
时,函数![]() 单调递增,则
单调递增,则![]() ;
;
当![]() 时,函数
时,函数![]() 单调递减,则
单调递减,则![]() ,即
,即![]() ;
;
当![]() 时,函数
时,函数![]() 单调递减,则
单调递减,则![]() .
.
综上所述,函数![]() 的最大值为
的最大值为![]() ,
,
由题知,![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.
A
在△ABC中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)求B的大小;
(2)若![]() 边上的中线
边上的中线![]() 的长为
的长为![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
(1)由![]() ,
,

![]()
因为![]()
所以![]() 由
由![]() ,则
,则![]() ,
,
(2)如图延长线段![]() 至
至![]() ,满足
,满足![]() ,联结
,联结![]() ,
,

在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由余弦定理可得![]() ,
,
即 ,
,
因为![]() ,
,
所以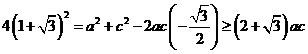 ,
,
则![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
那么![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
则![]() 面积的最大值为2.
面积的最大值为2.
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户刁子健分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。