为了打破国外的技术封锁,某公司很重视芯片的研究.为制定下一年的研发投入计划,需了解年研发资金投入量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数型:①
(单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数型:①![]() ,②
,②![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() 均为常数,
均为常数,![]() 为自然对数的底数.
为自然对数的底数.
现该公司收集了近12年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,
的数据,![]() ,并对这些数据作了初步处理,得到了下侧的散点图及一些统计量的值.令
,并对这些数据作了初步处理,得到了下侧的散点图及一些统计量的值.令![]() ,
,![]() ,
,![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
| 20 | 66 | 770 | 200 | 460 | 4.20 |

|
|
|
|
|
| 3125000 | 21500 | 0.308 | 14 |
(Ⅰ)设![]() 和
和![]() 的相关系数为
的相关系数为![]() ,
,![]() 和
和![]() 的相关系数为
的相关系数为![]() ,请从相关系数的角度,选择一个拟合程度更好的模型;
,请从相关系数的角度,选择一个拟合程度更好的模型;
(Ⅱ)(ⅰ)根据(Ⅰ)的选择及表中数据,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(ⅱ)若下一年销售额![]() 需达到90亿元,预测下一年的研发资金投入量是多少亿元?
需达到90亿元,预测下一年的研发资金投入量是多少亿元?
附:①相关系数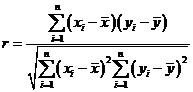 ,回归直线
,回归直线![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() ;
;
②参考数据:![]() ,
,![]() ,
,![]() .
.
解:(Ⅰ)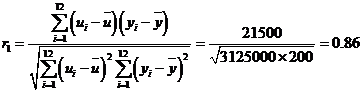 , 2分
, 2分
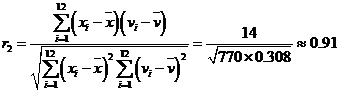 4分
4分
则![]() ,因此从相关系数的角度,模型
,因此从相关系数的角度,模型![]() 的拟合程度更好 5分
的拟合程度更好 5分
(Ⅱ)(ⅰ)由![]() ,得
,得![]() ,即
,即![]() .
.
由于 .
.
![]() , 7分
, 7分
∴![]() ,
,
所以![]() 8分
8分
(ⅱ)下一年销售额![]() 需达到90亿元,即
需达到90亿元,即![]() ,
,
代入![]() 得,
得,![]() , 10分
, 10分
又![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以预测下一年的研发资金投入量约是32.99亿元. 12分
已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(Ⅱ)若存在实数![]() ,对任意实数
,对任意实数![]() ,不等式
,不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)当![]() 时,不等式化为
时,不等式化为![]() .
.
则![]() 或
或![]() 或
或![]() , 3分
, 3分
即![]() 或
或![]() 或
或![]() ,
,
所以不等式的解集是![]() . -6分
. -6分
(Ⅱ)当![]() 时,
时,![]()
∴![]() 8分
8分
![]() ,
,
∴![]() . 10分
. 10分
据题意,![]() ,则
,则![]() ,
,
解得![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() . 12分
. 12分
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,射线
轴的非负半轴为极轴建立极坐标系,射线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出是何种曲线;
的极坐标方程,并指出是何种曲线;
(Ⅱ)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,射线
两点,射线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
解:(Ⅰ)由![]() (
(![]() 为参数)化为普通方程为
为参数)化为普通方程为![]() 2分
2分
![]() ,整理得极坐标方程为
,整理得极坐标方程为![]() 5分
5分
曲线![]() 是以
是以![]() 为圆心,2为半径的圆. 6分
为圆心,2为半径的圆. 6分
(Ⅱ)令![]() ,
,
![]() 8分
8分
![]() 10分
10分
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
![]() 面积的取值范围为
面积的取值范围为![]() 12分
12分
对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(Ⅰ)试给出这个常数![]() 的值(不需要证明);
的值(不需要证明);
(Ⅱ)在(Ⅰ)所得结论的条件下证明命题![]() .
.
解:(Ⅰ)令![]() 得:
得:![]() ,故
,故![]() ; 4分
; 4分
(Ⅱ)先证明![]() .
.
∵![]() ,
,![]() ,要证上式,只要证
,要证上式,只要证![]() ,
,
即证![]() ,即证
,即证![]() ,这显然成立.
,这显然成立.
∴![]() . 8分
. 8分
再证明![]() .
.
∵![]() ,
,![]() ,要证上式,只要证
,要证上式,只要证![]() ,
,
即证![]() ,即证
,即证![]() ,这显然成立.
,这显然成立.
∴![]() . 12分
. 12分
函数![]() .
.
(Ⅰ)求函数![]() 的最小值;
的最小值;
(Ⅱ)若![]() 的最小值为
的最小值为![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.
解:(Ⅰ)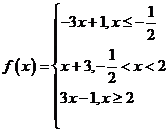 , 3分
, 3分
故当![]() 时
时![]() 最小值为
最小值为![]() 6分
6分
(Ⅱ)由①可知,![]() ,
,
由柯西不等式得:![]() 10分
10分
∴![]() ,当且仅当
,当且仅当![]() ,
,![]() 时等号成立 12分
时等号成立 12分
本卷还有19题,登录并加入会员即可免费使用哦~

该作品由: 用户czz分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。