已知正项数列{an}的前n项和为Sn,满足an2+an﹣2Sn=0(n∈N*).
(1)求数列{an}的通项公式;
(2)记数列{bn}的前n项和为Tn,若bn=(2an﹣7)•2n,求Tn;
(3)求数列{Tn}的最小项.
解:(1)由an2+an﹣2Sn=0,得到:![]() ,
,
两式相减得:![]() ,
,
整理得:(an+1+an)(an+1﹣an﹣1)=0,
由于数列{an}是正项数列,
所以an+1﹣an=1(常数),
当n=1时,解得a1=1.
故:an=1+n﹣1=n.
(2)由(1)得:![]() ,
,
所以:![]() ①,
①,
2![]() ②,
②,
①﹣②得:![]() ,
,
解得:![]() .
.
(3)![]() ,
,
当n≤2时,Tn+1<Tn,
当n≥3时,Tn+1>Tn,
故:T1>T2>T3<T4<T5<…,
故数列{Tn}的最小值为T3=﹣30.
【分析】(1)直接利用递推关系式的应用求出数列的通项公式.
(2)利用(1)的结论,进一步利用乘公比错位相减法的应用求出数列的和.
(3)利用数列的单调性的应用求出最小项.
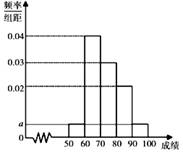
某校为了解高一年级学生的数学学科发展状况,随机抽取了100名学生,列出他们的高一第二学期期中考试数学成绩的频率分布直方图如图,其中成绩的分组区间为:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)利用样本估计总体的方法,估计该校高一年级此次期中考试的平均分(同一分组的成绩用该组区间的中点值做代表);
(3)若将分数从高分到低分排列,取前20%的同学评定为“优秀”档次,用样本估计总体的方法,估计本次期中考试“优秀”档次的分数线.
解:(1)由题意得:
(2a+0.02+0.03+0.04)×10=1,
解得a=0.005.
(2)估计该校此次期中考试平均分为:
55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73.
(3)由频率分布直方图可知:
区间[90,100]占5%,区间[80,90)占20%,
估计“优秀”档次的分数线为:
80+10×![]() =82.5.
=82.5.
【分析】(1)由频率分布直方图能求出a.
(2)由频率分布直设计图能估计该校此次期中考试平均分.
(3)由频率分布直方图估计“优秀”档次的分数线.
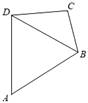
如图,在平面四边形ABCD中,若∠ADC=90°,sinA=![]() ,AB=8,BD=6.
,AB=8,BD=6.
(1)求∠ADB;
(2)若DC=2![]() ,求BC.
,求BC.
解:(1)在△ABD中,sinA=![]() ,AB=8,BD=6,
,AB=8,BD=6,
可得![]() =
=![]() ,即有sin∠ADB=
,即有sin∠ADB=![]() =
=![]() =
=![]() ,
,
可得锐角ADB为60°;
(2)在△BCD中,BD=6,CD=2![]() ,∠CDB=90°﹣60°=30°,
,∠CDB=90°﹣60°=30°,
可得BC2=DB2+DC2﹣2DC•DBcos∠CDB=36+12﹣2•2![]() •6•
•6•![]() =12,
=12,
可得BC=2![]() .
.

【分析】(1)在△ABD中,运用正弦定理,计算可得所求角;
(2)在△BCD中,运用余弦定理计算可得所求值.
已知函数f(x)=x2﹣(a+b)x+a.
(1)若关于x的不等式f(x)<0的解集为{x|1<x<2},求a,b的值;
(2)当b=1时,解关于x的不等式f(x)>0.
解:(1)由题意可得,1,2是x2﹣(a+b)x+a=0的两根,
所以![]() ,所以a=2,b=1,
,所以a=2,b=1,
(2)当b=1时,f(x)=x2﹣(a+1)x+a>0可得(x﹣a)(x﹣1)>0,
当a<1时,解可得x<a或x>1,
当a=1时,解可得,x≠1,
当a>1时,解可得x<1或x>a
综上可得,当a<1时,{x|x<a或x>1},
当a=1时,{x|x≠1},
当a>1时,{x|x<1或x>a}
【分析】(1)由题意可得,1,2是x2﹣(a+b)x+a=0的两根,然后结合方程的根与系数关系可求;
(2)当b=1时由已知可得(x﹣a)(x﹣1)>0,然后对a与1的大小进行讨论即可求解.
已知袋中装有5个小球,其中3个黑球记为A,B,C,2个红球记为a,b,现从中随机摸出两个球.
(1)写出所有的基本事件;
(2)求两个球中恰有一个黑球的概率;
(3)求两个球中至少有一个黑球的概率.
解:(1)袋中装有5个小球,其中3个黑球记为A,B,C,2个红球记为a,b,
现从中随机摸出两个球.以有序实数对表示摸球的结果,
所有的基本事件有10个,分别为:(A,B),(A,C),(A,a),(B,C),(B,a),(B,b),(C,a),(C,b),(a,b).
(2)记“两个球中恰有一个黑球”为事件M,则事件M包含的基本事件有6个,分别为:
(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),
∴两个球中恰有一个黑球的概率P(M)=![]() =
=![]() .
.
(3)设“两个球中至少有一个黑球”为事件N,
则事件N的对立事件![]() 为“两个球中没有黑球”,
为“两个球中没有黑球”,
事件![]() 包含的基本事件有:(a,b),只有1个,
包含的基本事件有:(a,b),只有1个,
∴两个球中至少有一个黑球的概率P(N)=1﹣P(![]() )=1﹣
)=1﹣![]() =
=![]() .
.
【分析】(1)袋中装有5个小球,其中3个黑球记为A,B,C,2个红球记为a,b,利用列举法能求出所有的基本事件.
(2)记“两个球中恰有一个黑球”为事件M,利用列举法求出事件M包含的基本事件有6个,由此能求出两个球中恰有一个黑球的概率.
(3)设“两个球中至少有一个黑球”为事件N,则事件N的对立事件![]() 为“两个球中没有黑球”,利用列举法求出事件
为“两个球中没有黑球”,利用列举法求出事件![]() 包含的基本事件只有1个,由此能求出两个球中至少有一个黑球的概率.
包含的基本事件只有1个,由此能求出两个球中至少有一个黑球的概率.
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户麦利分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。