已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,则
,则
A.a2=2b2 B.3a2=4b2 C.a=2b D.3a=4b
B
【分析】
由题意利用离心率的定义和![]() 的关系可得满足题意的等式.
的关系可得满足题意的等式.
【详解】
椭圆的离心率![]() ,化简得
,化简得![]() ,
,
故选B.
【点睛】
本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识、基本运算能力的考查.
已知实数![]() 成等比数列,则椭圆
成等比数列,则椭圆![]() 的离心率为
的离心率为
A.![]() B.2 C.
B.2 C.![]() 或2 D.
或2 D.![]() 或
或![]()
A
【分析】
由1,m,9构成一个等比数列,得到m=±3.当m=3时,圆锥曲线是椭圆;当m=﹣3时,圆锥曲线是双曲线,(舍)由此即可求出离心率.
【详解】
∵1,m,9构成一个等比数列,
∴m2=1×9,
则m=±3.
当m=3时,圆锥曲线![]() +y2=1是椭圆,它的离心率是
+y2=1是椭圆,它的离心率是![]() =
=![]() ;
;
当m=﹣3时,圆锥曲线![]() +y2=1是双曲线,故舍去,
+y2=1是双曲线,故舍去,
则离心率为![]() .
.
故选A.
【点睛】
本题考查圆锥曲线的离心率的求法,解题时要注意等比数列的性质的合理运用,注意分类讨论思想的灵活运用.
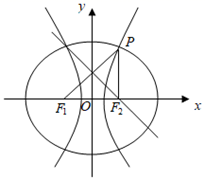
已知![]() 是椭圆与双曲线的公共焦点,P是它们的一个公共点,且
是椭圆与双曲线的公共焦点,P是它们的一个公共点,且![]() ,线段
,线段![]() 的垂直平分线过
的垂直平分线过![]() ,若椭圆的离心率为
,若椭圆的离心率为![]() ,双曲线的离心率为
,双曲线的离心率为![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.3 C.6 D.
B.3 C.6 D.![]()
C
【分析】
利用椭圆和双曲线的性质,用椭圆双曲线的焦距长轴长表示![]() ,再利用均值不等式得到答案.
,再利用均值不等式得到答案.
【详解】
设椭圆长轴![]() ,双曲线实轴
,双曲线实轴![]() ,由题意可知:
,由题意可知:![]() ,
,
又![]() ,
,![]() ,
,
两式相减,可得:![]() ,
,![]() ,
,
![]() . ,
. ,
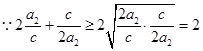 ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
![]() 的最小值为6,
的最小值为6,
故选:C.
【点睛】
本题考查了椭圆双曲线的性质,用椭圆双曲线的焦距长轴长表示![]() 是解题的关键,意在考查学生的计算能力.
是解题的关键,意在考查学生的计算能力.
设椭圆![]() 的焦点为
的焦点为![]() ,
,![]() 是椭圆上一点,且
是椭圆上一点,且![]() ,若
,若![]() 的外接圆和内切圆的半径分别为
的外接圆和内切圆的半径分别为![]() ,当
,当![]() 时,椭圆的离心率为( )
时,椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【解析】
分析:
详解:由椭圆![]() 的焦点为
的焦点为![]()
![]() 为椭圆上一点,且
为椭圆上一点,且![]() ,有
,有![]() 根据正弦定理
根据正弦定理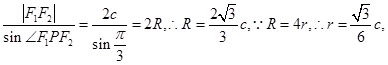 由余弦定理,
由余弦定理,![]() 由
由![]()
![]() ,可得
,可得![]() ,则由三角形面积公式
,则由三角形面积公式![]() 可得
可得![]()
故选B.
点睛:本题考查椭圆的离心率的求法,注意运用椭圆的定义和三角形的内切圆的半径的求法,以及正弦定理,余弦定理的应用,考查化简整理的运算能力,是中档题.
(2017新课标全国卷Ⅲ文科)已知椭圆C:![]() 的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线
的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线![]() 相切,则C的离心率为
相切,则C的离心率为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
A
【解析】
以线段![]() 为直径的圆的圆心为坐标原点
为直径的圆的圆心为坐标原点![]() ,半径为
,半径为![]() ,圆的方程为
,圆的方程为![]() ,
,
直线![]() 与圆相切,所以圆心到直线的距离等于半径,即
与圆相切,所以圆心到直线的距离等于半径,即![]() ,
,
整理可得![]() ,即
,即![]() 即
即![]() ,
,
从而![]() ,则椭圆的离心率
,则椭圆的离心率![]() ,
,
故选A.
【名师点睛】解决椭圆和双曲线的离心率的求值及取值范围问题,其关键就是确立一个关于![]() 的方程或不等式,再根据
的方程或不等式,再根据![]() 的关系消掉
的关系消掉![]() 得到
得到![]() 的关系式,而建立关于
的关系式,而建立关于![]() 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户陈红岩分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。