设![]() 是同一个半径为4的球的球面上四点,
是同一个半径为4的球的球面上四点,![]() 为等边三角形且其面积为
为等边三角形且其面积为![]() ,则三棱锥
,则三棱锥![]() 体积的最大值为
体积的最大值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【详解】
分析:作图,D为MO 与球的交点,点M为三角形ABC的中心,判断出当![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积最大,然后进行计算可得.
体积最大,然后进行计算可得.
详解:如图所示,
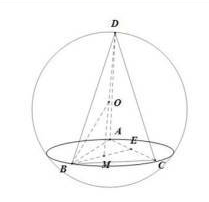
点M为三角形ABC的中心,E为AC中点,
当![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积最大
体积最大
此时,![]()
![]()
![]() ,
,
![]() 点M为三角形ABC的中心
点M为三角形ABC的中心
![]()
![]() 中,有
中,有![]()
![]()
![]()
故选B.
点睛:本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出当![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 体积最大很关键,由M为三角形ABC的重心,计算得到
体积最大很关键,由M为三角形ABC的重心,计算得到![]() ,再由勾股定理得到OM,进而得到结果,属于较难题型.
,再由勾股定理得到OM,进而得到结果,属于较难题型.
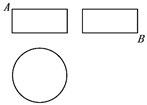
某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
B
【分析】
首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.
【详解】
根据圆柱的三视图以及其本身的特征,
将圆柱的侧面展开图平铺,
可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,
所以所求的最短路径的长度为![]() ,故选B.
,故选B.
点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.
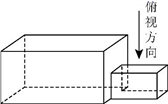
中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是
A. B.
B.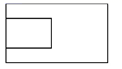 C.
C.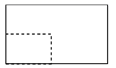 D.
D.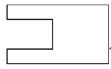
A
【详解】
详解:由题意知,题干中所给的是榫头,是凸出的几何体,求得是卯眼的俯视图,卯眼是凹进去的,即俯视图中应有一不可见的长方形,
且俯视图应为对称图形
故俯视图为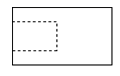
故选A.
点睛:本题主要考查空间几何体的三视图,考查学生的空间想象能力,属于基础题.
在长方体![]() 中,
中,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则该长方体的体积为( )
,则该长方体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
【分析】
首先画出长方体![]() ,利用题中条件,得到
,利用题中条件,得到![]() ,根据
,根据![]() ,求得
,求得![]() ,可以确定
,可以确定![]() ,之后利用长方体的体积公式求出长方体的体积.
,之后利用长方体的体积公式求出长方体的体积.
【详解】
在长方体![]() 中,连接
中,连接![]() ,
,
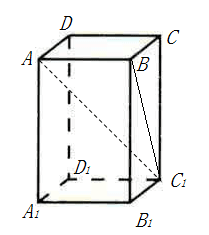
根据线面角的定义可知![]() ,
,
因为![]() ,所以
,所以![]() ,从而求得
,从而求得![]() ,
,
所以该长方体的体积为![]() ,故选C.
,故选C.
【点睛】
该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长就显得尤为重要,此时就需要明确线面角的定义,从而得到量之间的关系,从而求得结果.
已知圆柱的上、下底面的中心分别为![]() ,
,![]() ,过直线
,过直线![]() 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【解析】
分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积.
详解:根据题意,可得截面是边长为![]() 的正方形,
的正方形,
结合圆柱的特征,可知该圆柱的底面为半径是![]() 的圆,且高为
的圆,且高为![]() ,
,
所以其表面积为![]() ,故选B.
,故选B.
点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。