高中数学2021届专题复习——推理与证明训练题【含详解】
高中
整体难度：偏难
2020-12-09
题号
一
二
三
四
五
评分
一、选择题 (共49题)
添加该题型下试题
1.
在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．
甲：我的成绩比乙高．
乙：丙的成绩比我和甲的都高．
丙：我的成绩比乙高．
成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为
A．甲、乙、丙 B．乙、甲、丙
C．丙、乙、甲 D．甲、丙、乙
难度：
知识点：推理与证明
使用次数：151
【答案】
A
【分析】
利用逐一验证的方法进行求解.
【详解】
若甲预测正确，则乙、丙预测错误，则甲比乙成绩高，丙比乙成绩低，故3人成绩由高到低依次为甲，乙，丙；若乙预测正确，则丙预测也正确，不符合题意；若丙预测正确，则甲必预测错误，丙比乙的成绩高，乙比甲成绩高，即丙比甲，乙成绩都高，即乙预测正确，不符合题意，故选A．
【点睛】
本题将数学知识与时政结合，主要考查推理判断能力．题目有一定难度，注重了基础知识、逻辑推理能力的考查．
2.
甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则( )
A．乙可以知道四人的成绩 B．丁可以知道四人的成绩
C．乙、丁可以知道对方的成绩 D．乙、丁可以知道自己的成绩
难度：
知识点：推理与证明
使用次数：193
【答案】
D
【解析】
根据四人所知只有自己看到，老师所说及最后甲说话，继而可以推出正确答案
【详解】
解：四人所知只有自己看到，老师所说及最后甲说话，
甲不知自己的成绩
→乙丙必有一优一良，（若为两优，甲会知道自己的成绩；若是两良，甲也会知道自己的成绩）
→乙看到了丙的成绩，知自己的成绩
→丁看到甲、丁也为一优一良，丁知自己的成绩，
给甲看乙丙成绩，甲不知道自已的成绩，说明乙丙一优一良，假定乙丙都是优，则甲是良，假定乙丙都是良，则甲是优，那么甲就知道自已的成绩了．给乙看丙成绩，乙没有说不知道自已的成绩，假定丙是优，则乙是良，乙就知道自己成绩．给丁看甲成绩，因为甲不知道自己成绩，乙丙是一优一良，则甲丁也是一优一良，丁看到甲成绩，假定甲是优，则丁是良，丁肯定知道自已的成绩了
故选：D．
【点睛】
本题考查了合情推理的问题，关键掌握四人所知只有自己看到，老师所说及最后甲说话，属于中档题．
3.
某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图．图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃．下面叙述不正确的是 ( )
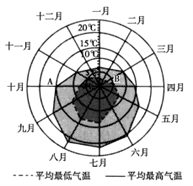
A．各月的平均最低气温都在0℃以上
B．七月的平均温差比一月的平均温差大
C．三月和十一月的平均最高气温基本相同
D．平均最高气温高于20℃的月份有5个
难度：
知识点：推理与证明
使用次数：112
【答案】
D
【解析】
试题分析：由图可知各月的平均最低气温都在0℃以上，A正确；由图可知在七月的平均温差大于
，而一月的平均温差小于
，所以七月的平均温差比一月的平均温差大，B正确；由图可知三月和十一月的平均最高气温都大约在
，基本相同，C正确；由图可知平均最高气温高于20℃的月份有7，8两个月，所以不正确．故选D．
【考点】
统计图
【易错警示】
解答本题时易错可能有两种：（1）对图形中的线条认识不明确，不知所措，只觉得是两把雨伞重叠在一起，找不到解决问题的方法；（2）估计平均温差时易出现错误，错选B．
4.
用数学归纳法证明
，则当
时，左端应在
的基础上加上（ ）
A．
B．
C．
D．
难度：
知识点：推理与证明
使用次数：183
【答案】
C
【分析】
首先分析题目求用数学归纳法证明1+2+3+…+n2=
时，当n=k+1时左端应在n=k的基础上加上的式子，可以分别使得n=k，和n=k+1代入等式，然后把n=k+1时等式的左端减去n=k时等式的左端，即可得到答案．
【详解】
当n=k时，等式左端=1+2+…+k2，
当n=k+1时，等式左端=1+2+…+k2+k2+1+k2+2+…+（k+1）2，增加了项（k2+1）+（k2+2）+（k2+3）+…+（k+1）2．
故选C．
【点睛】
本题主要考查数学归纳法，属于中档题./
5.
我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就.在“杨辉三角”中，第
行的所有数字之和为
，若去除所有为1的项，依次构成数列
，则此数列的前55项和为( )
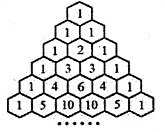
A．4072 B．2026 C．4096 D．2048
难度：
知识点：数列
使用次数：145
【答案】
A
【分析】
利用n次二项式系数对应杨辉三角形的第n+1行，然后令x＝1得到对应项的系数和，结合等比数列和等差数列的公式进行转化求解即可．
【详解】
解：由题意可知：每一行数字和为首项为1，公比为2的等比数列，
则杨辉三角形的前n项和为Sn
2n﹣1，
若去除所有的为1的项，则剩下的每一行的个数为1，2，3，4，……，可以看成构成一个首项为1，公差为1的等差数列，
则Tn
，
可得当n＝10，所有项的个数和为55，
则杨辉三角形的前12项的和为S12＝212﹣1，
则此数列前55项的和为S12﹣23＝4072，
故选A．
【点睛】
本题主要考查归纳推理的应用，结合杨辉三角形的系数与二项式系数的关系以及等比数列等差数列的求和公式是解决本题的关键，综合性较强，难度较大．
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
28
28.00%
容易
12
12.0%
偏难
37
37.0%
基础
10
10.0%
很难
13
13.0%
题型统计
大题类型
数量
占比
选择题
49
49.0%
解答题
29
28.99%
填空题
22
22.0%
知识点统计
知识点
数量
占比
推理与证明
49
49.0%
数列
23
23.0%
三角函数
4
4.0%
不等式选讲
1
1.0%
不等式
7
7.00%
空间几何体
1
1.0%
集合与函数的概念
2
2.0%
数系的扩充与复数的引入
1
1.0%
导数及其应用
7
7.00%
基本初等函数I
2
2.0%
计数原理
1
1.0%
概率
1
1.0%
点 直线 平面之间的位置
1
1.0%
版权提示
该作品由: 用户王啸天分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。