已知随机变量![]() ,
,![]() ,则
,则![]() ( )
( )
A.0.16 B.0.32 C.0.34 D.0.68
C
【分析】
先由对称性求出![]() ,再利用
,再利用![]() 即得解.
即得解.
【详解】
解:![]() 关于
关于![]() 对称,
对称,
故![]() ,
,
![]()
![]()
故选:C
【点睛】
考查正态分布在给定区间的概率,基础题.
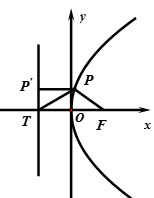
已知抛物线C:![]() (p>0)的焦点为F,对称轴与准线的交点为T,P为C上任意一点,若
(p>0)的焦点为F,对称轴与准线的交点为T,P为C上任意一点,若![]() ,则∠PTF=( )
,则∠PTF=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【分析】
过点![]() 做抛物线准线的垂线,垂直为
做抛物线准线的垂线,垂直为![]() ,根据抛物线的定义,结合条件,可求出
,根据抛物线的定义,结合条件,可求出![]() ,而
,而![]() =
=![]() ,即可求解.
,即可求解.
【详解】
过点![]() 做抛物线准线的垂线,垂足为
做抛物线准线的垂线,垂足为![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.
故选:A.
【点睛】
本题考查抛物线定义的应用,正确理解抛物线的点到准线和到焦点的距离相等,是解题的关键,属于基础题.
复数![]() (
(![]() ,
,![]() 是虚数单位)在复平面上对应的点不可能位于( ).
是虚数单位)在复平面上对应的点不可能位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
A
【分析】
利用复数代数形式的乘除运算化简,由实部和虚部不同时大于0说明![]() 在复平面上对应的点不可能位于第一象限.
在复平面上对应的点不可能位于第一象限.
【详解】
解:![]()
![]() ,
,
![]() 在复平面上对应的点的坐标为
在复平面上对应的点的坐标为![]() ,
,
若![]() ,则
,则![]() ,
,
![]() .
.
![]() 在复平面上对应的点不可能位于第一象限.
在复平面上对应的点不可能位于第一象限.
故选:![]() .
.
【点睛】
本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,属于基础题.
现有4名男生,2名女生.从中选出3人参加学校组织的社会实践活动,在男生甲被选中的情况下,女生乙也被选中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
D
【分析】
设男生甲被选中为事件![]() ,女生乙也被选中为事件
,女生乙也被选中为事件![]() ,分别求得
,分别求得![]() ,
,![]() ,再结合条件概率的计算公式,即可求解.
,再结合条件概率的计算公式,即可求解.
【详解】
由题意,从现有4名男生,2名女生选出3人参加学校组织的社会实践活动,
设男生甲被选中为事件![]() ,其概率为
,其概率为![]() ,
,
设女生乙也被选中为事件![]() ,其概率为
,其概率为![]() ,
,
所以在男生甲被选中的情况下,女生乙也被选中的概率为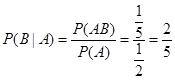 .
.
故选:D.
【点睛】
本题主要考查了条件概率的求解,其中解答中正确理解题意,熟练应用条件概率的计算公式求解是解答的关键,着重考查推理与计算能力.
已知等比数列![]() 中,
中,![]() ,则“
,则“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A
【分析】
结合等比数列通项公式可求得![]() 的范围,可验证充分性和必要性是否成立,由此得到结果.
的范围,可验证充分性和必要性是否成立,由此得到结果.
【详解】
设等比数列![]() 的公比为
的公比为![]() ,
,
由![]() 得:
得:![]() ,又
,又![]() ,
,![]() ,解得:
,解得:![]() ,
,
![]() ,充分性成立;
,充分性成立;
由![]() 得:
得:![]() ,又
,又![]() ,
,![]() ,解得:
,解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,必要性不成立.
,必要性不成立.
![]() “
“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
故选:![]() .
.
【点睛】
本题考查充分条件与必要条件的判定,涉及到等比数列通项公式的应用,属于基础题.
本卷还有40题,登录并加入会员即可免费使用哦~

该作品由: 用户bxg分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。