高中数学2020年年末周练知识点——圆与方程训练题（一）【含详解】
高中
整体难度：中等
2020-12-29
题号
一
二
三
四
五
评分
一、选择题 (共56题)
添加该题型下试题
1.
已知圆
的方程为
，点
在直线
上，线段
为圆的直径，则
的最小值为（）
A．2 B．
C．3 D．
难度：
知识点：平面向量
使用次数：142
【答案】
B
【分析】
将
转化为
，利用圆心到直线的距离求得
的取值范围求得的最小值.
【详解】
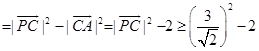
.故选B.
【点睛】
本小题主要考查向量的线性运算，考查点到直线距离公式，考查化归与转化的数学思想方法，属于中档题.
2.
直线
分别与
轴，
轴交于
，
两点，点在圆
上，则
面积的取值范围是
A．
B．
C．
D．
难度：
知识点：圆与方程
使用次数：118
【答案】
A
【解析】
分析：先求出A，B两点坐标得到
再计算圆心到直线距离，得到点P到直线距离范围，由面积公式计算即可
详解：
直线
分别与
轴，
轴交于
，
两点
,则
点P在圆
上
圆心为（2，0），则圆心到直线距离
故点P到直线的距离
的范围为
则
故答案选A.
点睛：本题主要考查直线与圆，考查了点到直线的距离公式，三角形的面积公式，属于中档题．
3.
圆
的圆心到直线
的距离为1，则
（ ）
A．
B．
C．
D．2
难度：
知识点：圆与方程
使用次数：197
【答案】
A
【解析】
试题分析：由
配方得
，所以圆心为
，因为圆的圆心到直线
的距离为1，所以
，解得
，故选A.
【考点】 圆的方程，点到直线的距离公式
【名师点睛】直线与圆的位置关系有三种情况：相交、相切和相离. 已知直线与圆的位置关系时，常用几何法将位置关系转化为圆心到直线的距离d与半径r的大小关系，以此来确定参数的值或取值范围．
4.
若过点（2，1）的圆与两坐标轴都相切，则圆心到直线
的距离为（ ）
A．
B．
C．
D．
难度：
知识点：圆与方程
使用次数：117
【答案】
B
【分析】
由题意可知圆心在第一象限，设圆心的坐标为
，可得圆的半径为
，写出圆的标准方程，利用点
在圆上，求得实数的值，利用点到直线的距离公式可求出圆心到直线
的距离.
【详解】
由于圆上的点在第一象限，若圆心不在第一象限，
则圆与至少与一条坐标轴相交，不合乎题意，所以圆心必在第一象限，
设圆心的坐标为
，则圆的半径为，
圆的标准方程为
.
由题意可得
，
可得
，解得
或
，
所以圆心的坐标为
或
，
圆心
到直线
的距离均为
；
圆心
到直线的距离均为
圆心到直线的距离均为
；
所以，圆心到直线的距离为
.
故选：B.
【点睛】
本题考查圆心到直线距离的计算，求出圆的方程是解题的关键，考查计算能力，属于中等题.
5.
在平面直角坐标系中，记
为点
到直线
的距离，当
、
变化时，的最大值为（ ）
A．
B．
C．
D．
难度：
知识点：直线与方程
使用次数：165
【答案】
C
【分析】
为单位圆上一点，而直线
过点
，则根据几何意义得
的最大值为
.
【详解】
为单位圆上一点，而直线过点，
所以的最大值为
，选C.
【点睛】
与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面．解决此类问题的主要思路是利用圆的几何性质将问题转化．
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
中等
55
55.00%
容易
18
18.0%
偏难
21
21.0%
基础
5
5.0%
很难
1
1.0%
题型统计
大题类型
数量
占比
选择题
56
56.00%
解答题
28
28.00%
填空题
16
16.0%
知识点统计
知识点
数量
占比
平面向量
6
6.0%
圆与方程
72
72.0%
直线与方程
16
16.0%
不等式
3
3.0%
导数及其应用
1
1.0%
圆锥曲线与方程
1
1.0%
三角函数
1
1.0%
版权提示
该作品由: 用户cf分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。