2019年末,武汉出现新型冠状病毒肺炎(![]() )疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为
)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为![]() (
(![]() )且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
)且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,则
最大,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【分析】
根据题意分别求出事件A:检测5个人确定为“感染高危户”发生的概率和事件B:检测6个人确定为“感染高危户”发生的概率,即可得出![]() 的表达式,再根据基本不等式即可求出.
的表达式,再根据基本不等式即可求出.
【详解】
设事件A:检测5个人确定为“感染高危户”,
事件B:检测6个人确定为“感染高危户”,
∴![]() ,
,![]() .
.
即![]()
设![]() ,则
,则![]()
∴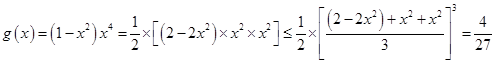
当且仅当![]() 即
即![]() 时取等号,即
时取等号,即![]() .
.
故选:A.
【点睛】
本题主要考查概率的计算,涉及相互独立事件同时发生的概率公式的应用,互斥事件概率加法公式的应用,以及基本不等式的应用,解题关键是对题意的理解和事件的分解,意在考查学生的数学运算能力和数学建模能力,属于较难题.
如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从![]() 中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
【详解】
试题分析:从![]() 中任取3个不同的数共有10种不同的取法,其中的勾股数只有3,4,5,故3个数构成一组勾股数的取法只有1种,故所求概率为
中任取3个不同的数共有10种不同的取法,其中的勾股数只有3,4,5,故3个数构成一组勾股数的取法只有1种,故所求概率为![]() ,故选C.
,故选C.
考点:古典概型
某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
C
【分析】
记“该中学学生喜欢足球”为事件![]() ,“该中学学生喜欢游泳”为事件
,“该中学学生喜欢游泳”为事件![]() ,则“该中学学生喜欢足球或游泳”为事件
,则“该中学学生喜欢足球或游泳”为事件![]() ,“该中学学生既喜欢足球又喜欢游泳”为事件
,“该中学学生既喜欢足球又喜欢游泳”为事件![]() ,然后根据积事件的概率公式
,然后根据积事件的概率公式![]()
![]() 可得结果.
可得结果.
【详解】
记“该中学学生喜欢足球”为事件![]() ,“该中学学生喜欢游泳”为事件
,“该中学学生喜欢游泳”为事件![]() ,则“该中学学生喜欢足球或游泳”为事件
,则“该中学学生喜欢足球或游泳”为事件![]() ,“该中学学生既喜欢足球又喜欢游泳”为事件
,“该中学学生既喜欢足球又喜欢游泳”为事件![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以![]()
![]()
![]()
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为![]() .
.
故选:C.
【点睛】
本题考查了积事件的概率公式,属于基础题.
在区间![]() 上随机地取一个数
上随机地取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为( )
”发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【解析】
由![]() 得,
得,![]() ,所以,由几何概型概率的计算公式得,
,所以,由几何概型概率的计算公式得, ,故选
,故选![]() .
.
考点:1.几何概型;2.对数函数的性质.
如图,在直角坐标系![]() 中,过坐标原点
中,过坐标原点![]() 作曲线
作曲线![]() 的切线,切点为
的切线,切点为![]() ,过点
,过点![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,向矩形
,向矩形![]() 中随机撒一粒黄豆,则它落到阴影部分的概率为( )
中随机撒一粒黄豆,则它落到阴影部分的概率为( )
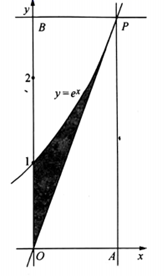
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【分析】
先设出切点![]() ,利用切线过原点求出切点P的坐标,再用积分求出阴影部分的面积,最后用几何概型求得结果.
,利用切线过原点求出切点P的坐标,再用积分求出阴影部分的面积,最后用几何概型求得结果.
【详解】
设切点![]() ,
,![]()
所以切线方程![]() ,又因为过原点
,又因为过原点
所以![]() 解得
解得![]()
所以点P![]()
因为![]() 与
与![]() 轴在
轴在![]() 围成的面积是
围成的面积是![]()
则阴影部分的面积为![]()
而矩形![]() 的面积为
的面积为![]()
故向矩形![]() 中随机撒一粒黄豆,则它落到阴影部分的概率为
中随机撒一粒黄豆,则它落到阴影部分的概率为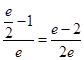
故选A
【点睛】
本题主要考查了几何概型,但是解题的关键是在于对于切点和积分的运用是否熟练,属于中档题.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户王生云分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。