高中数学2020年年末周练知识点——统计训练题（一）【含详解】
高中
整体难度：中等
2021-01-06
题号
一
二
三
四
五
评分
一、选择题 (共47题)
添加该题型下试题
1.
某单位有员工120人，其中女员工有72人，为做某项调查，拟采用分层抽样抽取容量为15的样本，则男员工应选取的人数是（ ）
A．5 B．6 C．7 D．8
难度：
知识点：统计案例
使用次数：136
【答案】
B
【解析】
试题分析：男员工应抽取的人数为
，故选B.
考点：分层抽样.
【方法点晴】本题主要考查了分层抽样方法及其应用，分层抽样中各层抽取个数依据各层个体数之比来分配，这是分层抽样的最主要的特点，首先各确定分层抽样的个数，分层后，各层的抽取一定要考虑到个体数目，选取不同的抽样方法，但一定要注意按比例抽取，牢记分层抽样的特点和方法是解答的关键，着重考查了学生的分析问题和解答问题的能力．
2.
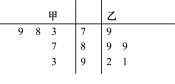
甲、乙两位同学在高一年级的5次考试中，数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别是
，则下列叙述正确的是（ ）
A．
，乙比甲成绩稳定
B．，甲比乙成绩稳定
C．
，乙比甲成绩稳定
D．，甲比乙成绩稳定
难度：
知识点：统计案例
使用次数：128
【答案】
C
【解析】
甲的平均成绩
，甲的成绩的方差
；
乙的平均成绩
，乙的成绩的方差
.
∴
，乙比甲成绩稳定.
故选C.
3.
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x/cm | 160 | 165 | 170 | 175 | 180 |
| 体重y/kg | 63 | 66 | 70 | 72 | 74 |
根据上表可得回归直线方程
=0.56x+
,据此模型预报身高为172 cm的高三男生的体重为( )
A．70.09 kg B．70.12 kg
C．70.55 kg D．71.05 kg
难度：
知识点：统计案例
使用次数：129
【答案】
B
【解析】
试题分析：由表中数据可得．
，
，
∵
一定在回归直线方程
上，
∴69=0．56×170+a，
解得a=-16．2
∴y=0．56x-16．2，
当x=172时，y=0．56×172-16．2=70．12
考点：线性回归方程
4.
演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是
A．中位数 B．平均数
C．方差 D．极差
难度：
知识点：统计案例
使用次数：196
【答案】
A
【分析】
可不用动笔，直接得到答案，亦可采用特殊数据，特值法筛选答案．
【详解】
设9位评委评分按从小到大排列为
．
则①原始中位数为
，去掉最低分
，最高分
，后剩余
，
中位数仍为，
A正确．
②原始平均数
，后来平均数
平均数受极端值影响较大，
与
不一定相同，B不正确
③
由②易知，C不正确．
④原极差
，后来极差
可能相等可能变小，D不正确．
【点睛】
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
5.
某学校为了解1 000名新生的身体素质，将这些学生编号为1，2，…，1 000，从这些新生中用系统抽样方法等距抽取100名学生进行体质测验，若46号学生被抽到，则下面4名学生中被抽到的是
A．8号学生 B．200号学生 C．616号学生 D．815号学生
难度：
知识点：统计案例
使用次数：139
【答案】
C
【分析】
等差数列的性质．渗透了数据分析素养．使用统计思想，逐个选项判断得出答案．
【详解】
详解：由已知将1000名学生分成100个组，每组10名学生，用系统抽样，46号学生被抽到，
所以第一组抽到6号，且每组抽到的学生号构成等差数列
，公差
，
所以
，
若
，则
，不合题意；若
，则
，不合题意；
若
，则
，符合题意；若
，则
，不合题意．故选C．
【点睛】
本题主要考查系统抽样.
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
基础
13
13.0%
中等
61
61.0%
容易
22
22.0%
很难
1
1.0%
偏难
3
3.0%
题型统计
大题类型
数量
占比
选择题
47
47.0%
解答题
44
44.0%
填空题
9
9.0%
知识点统计
知识点
数量
占比
统计案例
94
94.0%
统计
5
5.0%
框图
1
1.0%
版权提示
该作品由: 用户汪良山分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。