已知函数![]() ,其中a为常数.
,其中a为常数.
(1)若f(x)的图象在x=1处的切线经过点(3,4),求实数a的值;
(2)若0<a<1,求证: ;
;
(3)当函数存在三个不同的零点时,求实数a的取值范围
(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【详解】
试题分析:(1)根据导数的几何意义可得:![]() ,再结合斜率公式
,再结合斜率公式![]() 进而得出
进而得出![]() 的值;(2)表示出
的值;(2)表示出![]() ,然后构造函数
,然后构造函数![]() 通过讨论函数的单调性证明
通过讨论函数的单调性证明![]() ;(3)将函数零点的问题转化为函数图像与
;(3)将函数零点的问题转化为函数图像与![]() 轴交点个数的问题,通过导数讨论函数的单调性来解决.
轴交点个数的问题,通过导数讨论函数的单调性来解决.
试题解析:由题知![]()
(Ⅰ)![]()
![]()
![]()
![]()
(Ⅱ)![]() ,令
,令![]() ,
,
则![]()
∴![]() 时,
时,![]() 单调递减,
单调递减,
故![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]()
(Ⅲ)![]()
①![]()
∴![]() 至多只有一个零点,不合题意;
至多只有一个零点,不合题意;
②![]()
∴![]() 至多只有一个零点,不合题意;
至多只有一个零点,不合题意;
③![]()
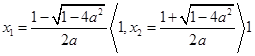
此时,![]() 在
在![]() 上递减,
上递减,![]() 上递增,
上递增,![]() 上递减,所以,
上递减,所以,![]() 至多有三个零点.因为
至多有三个零点.因为![]() 在
在![]() 递增,所以
递增,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,使得
,使得![]() ,又
,又![]() ,所以恰有三个不同零点:
,所以恰有三个不同零点:![]() ,所以函数
,所以函数![]() 存在三个不同的零点时,
存在三个不同的零点时,![]() 的取值范围是
的取值范围是![]() .
.
考点:函数与导数综合应用.
对于数列![]() ,若存在常数M>0,对任意的n∈N*,恒有
,若存在常数M>0,对任意的n∈N*,恒有![]() ,则称数列
,则称数列![]() 为B-数列.
为B-数列.
(1)首项为1,公比q(![]() )的等比数列是否为B-数列?请说明理由;
)的等比数列是否为B-数列?请说明理由;
(2)设Sn是数列{xn}的前n项和,给出下列两组论断:
A组:①数列{xn}是B-数列,②数列{xn}不是B-数列
B组:①数列{Sn}是B-数列,②数列{Sn}不是B-数列
请以其中一组的一个论断为条件,另一组的一个论断为结论组成一个命题.判断所给命题的真假,并证明你的结论.
(3)若数列{an}、![]() 都是B-数列,证明:数列{anbn}也是B-数列
都是B-数列,证明:数列{anbn}也是B-数列
(1)是B-数列(2)命题1为假命题. 命题2为真命题.(3)见解析
【详解】
解:(1)设满足条件的等比数列为{an},则![]() .于是
.于是
![]()
因此,![]()
因为|q|<1,所以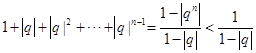
即![]()
故首项为1,公比q(|q|<1)的等比数列是B-数列.
(2)命题1:若数列{xn}是B-数列,则数列{Sn}也是B-数列此命题为假命题.
事实上,设x=1,n∈N*,易知数列{xn}是B-数列,但Sn=n,
此时![]() .
.
由n的任意性,知数列{Sn}不是B-数列
命题2:若数列{Sn}是B-数列,则数列{xn}也是B-数列此命题为真命题.
事实上,因为数列{Sn}是B-数列,所以存正数M,对任意n∈N*有
![]()
即![]() .于是
.于是
![]()
![]()
所以数列{xn}是B-数列
按题中要求组成其它命题时,仿上述解法即可获得解决.
(3)若数列{an}、{bn}都是B-数列,则存在正数M1,M2,使得对任意n∈N*,有
![]() ,
,
![]() .
.
注意到![]()
![]()
同理,可得![]() .记
.记![]() ,则有
,则有
![]()
![]()
因此,![]()
![]() .
.
故数列数列{anbn}是B-数列.
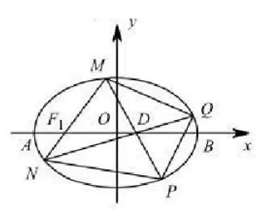
如图,在平面直角坐标系xOy中,已知点F1、F2分别为椭圆E:![]() 的左、右焦点,A,B分别是椭圆E的左、右顶点,D(1,0)为线段OF2的中点,且
的左、右焦点,A,B分别是椭圆E的左、右顶点,D(1,0)为线段OF2的中点,且![]() .
.
(1)求椭圆E的方程;
(2)若M为椭圆上的动点(异于A、B),连接MF1并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于点P、Q,连接PQ设直线MN、PQ的斜率存在且分别为k1、k2,试问题是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)![]() (2)-
(2)-![]()
【解析】
(1)∵![]() +5
+5![]() =0,∴
=0,∴![]() =5
=5![]() .∴a+c=5(a-c),化简得2a=3c,故椭圆E的离心率为
.∴a+c=5(a-c),化简得2a=3c,故椭圆E的离心率为![]() .
.
(2)存在满足条件的常数λ,λ=-![]() .点D(1,0)为线段OF2的中点,∴c=2,从而a=3,b=
.点D(1,0)为线段OF2的中点,∴c=2,从而a=3,b=![]() ,左焦点F1(-2,0),椭圆E的方程为
,左焦点F1(-2,0),椭圆E的方程为![]() =1,设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),则直线MD的方程为x=
=1,设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),则直线MD的方程为x=![]() y+1,代入椭圆方程
y+1,代入椭圆方程![]() =1,整理得,
=1,整理得,![]() y2+
y2+![]() y-4=0.∵y1+y3=
y-4=0.∵y1+y3=![]() ,∴y3=
,∴y3=![]() .从而x3=
.从而x3=![]() ,故点P
,故点P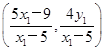 .同理,点Q
.同理,点Q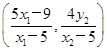 .∵三点M、F1、N共线,∴
.∵三点M、F1、N共线,∴![]() ,从而x1y2-x2y1=2(y1-y2).从而k2=
,从而x1y2-x2y1=2(y1-y2).从而k2=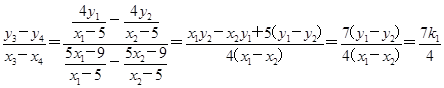 ,故k1-
,故k1-![]() =0,从而存在满足条件的常数λ=-
=0,从而存在满足条件的常数λ=-![]()
设f(x)是定义在区间(1,+∞)上的函数,其导函数为![]() .如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得
.如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得![]() =h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数![]() ,其中b为实数.
,其中b为实数.
①求证:函数f(x)具有性质P(a).②求函数f(x)的单调区间.
(2)已知函数g(x)具有性质P(2),给定x1,x2∈(1,+∞),x1<x2.设m为实数, ![]() ,且
,且![]() .若
.若![]() ,求实数m的取值范围
,求实数m的取值范围
(1)当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,![]() ),单调增区间为(
),单调增区间为(![]() ,+∞).
,+∞).
(2)(0,1)
【解析】
解:(1)由f(x)=ln x+![]() ,得f′(x)=
,得f′(x)=![]() .
.
①证明:因为x>1时,h(x)=![]() >0,所以函数f(x)具有性质P(b).
>0,所以函数f(x)具有性质P(b).
②当b≤2时,由x>1得x2-bx+1≥x2-2x+1=(x-1)2>0,
所以f′(x)>0.从而函数f(x)在区间(1,+∞)上单调递增.
当b>2时,令x2-bx+1=0得
x1=![]() ,x2=
,x2=![]() .
.
因为x1=![]() =
=![]() <
<![]() <1,
<1,
x2=![]() >1,
>1,
所以当x∈(1,x2)时,f′(x)<0;当x∈(x2,+∞)时,f′(x)>0;当x=x2时,f′(x)=0.从而函数f(x)在区间(1,x2)上单调递减,在区间(x2,+∞)上单调递增.
综上所述,当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,![]() ),单调增区间为(
),单调增区间为(![]() ,+∞).
,+∞).
(2)由题设知,g(x)的导函数
g′(x)=h(x)(x2-2x+1),
其中函数h(x)>0对于任意的x∈(1,+∞)都成立,
所以当x>1时,g′(x)=h(x)(x-1)2>0,
从而g(x)在区间(1,+∞)上单调递增.
①当m∈(0,1)时,
有α=mx1+(1-m)x2>mx1+(1-m)x1=x1,
α<mx2+(1-m)x2=x2,即α∈(x1,x2),
同理可得β∈(x1,x2).
所以由g(x)的单调性知g(α),g(β)∈(g(x1),g(x2)),从而有|g(α)-g(β)|<|g(x1)-g(x2)|,符合题意.
②当m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=(1-m)x1+mx2≤(1-m)x1+mx1=x1,于是由α>1,β>1及g(x)的单调性知g(β)≤g(x1)<g(x2)≤g(α),
所以|g(α)-g(β)|≥|g(x1)-g(x2)|,与题意不符.
③当m≥1时,同理可得α≤x1,β≥x2,
进而得|g(α)-g(β)|≥|g(x1)-g(x2)|,与题意不符.
综上所述,所求的m的取值范围为(0,1).
设x,y,z为非零实数,满足xy+yz+zx=1,证明:![]() .
.
不等式的证明一般可以考虑运用作差法或者是利用分析法来证明.
【解析】
试题分析:为使所证式有意义,![]() 三数中至多有一个为0;据对称性,不妨设
三数中至多有一个为0;据对称性,不妨设![]() ,则
,则![]() ;
;
![]() 、当
、当![]() 时,条件式成为
时,条件式成为![]() ,
,![]() ,
,![]() ,而
,而
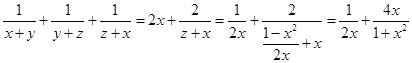 ,
,
只要证,![]() ,即
,即![]() ,也即
,也即![]() ,此为显然;取等号当且仅当
,此为显然;取等号当且仅当![]() .
.
![]() 、再证,对所有满足
、再证,对所有满足![]() 的非负实数
的非负实数![]() ,皆有
,皆有
![]() .显然,三数
.显然,三数![]() 中至多有一个为0,据对称性,
中至多有一个为0,据对称性,
仍设![]() ,则
,则![]() ,令
,令![]() ,
,![]() 为锐角,以
为锐角,以![]() 为内角,构作
为内角,构作![]() ,则
,则![]()
![]() ,于是
,于是![]() ,且由
,且由![]() 知,
知,![]() ;于是
;于是![]() ,即
,即![]() 是一个非钝角三角形.
是一个非钝角三角形.
下面采用调整法,对于任一个以![]() 为最大角的非钝角三角形
为最大角的非钝角三角形![]() ,固定最大角
,固定最大角![]() ,将
,将![]() 调整为以
调整为以![]() 为顶角的等腰
为顶角的等腰![]() ,其中
,其中![]() ,且设
,且设![]() ,记
,记![]() ,据
,据![]() 知,
知,
![]() .今证明,
.今证明,![]() .即
.即![]()
……①.
即要证![]() ……②
……②
先证![]() ……③,即证
……③,即证![]() ,
,
即 ,此即
,此即![]() ,也即
,也即
![]() ,即
,即![]() ,此为显然.
,此为显然.
由于在![]() 中,
中,![]() ,则
,则 ;而在
;而在![]() 中,
中,
![]() ,因此②式成为
,因此②式成为
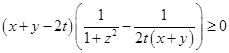 ……④,
……④,
只要证,![]() ……⑤,即证
……⑤,即证![]() ,注意③式以及
,注意③式以及
![]() ,只要证
,只要证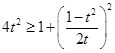 ,即
,即![]() ,也即
,也即![]() …⑥
…⑥
由于最大角![]() 满足:
满足:![]() ,而
,而![]() ,则
,则![]() ,所以
,所以
![]() ,故⑥成立,因此⑤得证,由③及⑤得④成立,从而①成立,即
,故⑥成立,因此⑤得证,由③及⑤得④成立,从而①成立,即![]() ,因此本题得证.
,因此本题得证.
考点:不等式的证明
点评:主要是考查了不等式的证明,方法比较多,一般是分析法和作差法构造函数法,属于难度题.

该作品由: 用户黄郑分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。