设函数![]()
(1)解不等式![]() ;
;
(2)若![]() 的取值范围。
的取值范围。
答案
解:(1)∵
∴当x<1时,3-2x>3,解得x<0;
当1![]() 无解
无解
当x>2时2x-3>3,解得x<3.
综上,x<0或x>3,
∴不等式f(x)>3的解集为![]()
(2)∵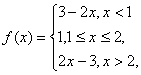
∴![]()
∵![]() 恒成立
恒成立
∴a<1,即实数a的取值范围是![]()
设函数![]()
(1)解不等式![]() ;
;
(2)若![]() 的取值范围。
的取值范围。
解:(1)∵
∴当x<1时,3-2x>3,解得x<0;
当1![]() 无解
无解
当x>2时2x-3>3,解得x<3.
综上,x<0或x>3,
∴不等式f(x)>3的解集为![]()
(2)∵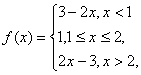
∴![]()
∵![]() 恒成立
恒成立
∴a<1,即实数a的取值范围是![]()
绝对值不等式:
当a>0时,有 ;
; 或x<-a 。
或x<-a 。
 ;
; 或x<-a
或x<-a 
登录并加入会员可无限制查看知识点解析