已知点G是圆F:![]() 上任意一点,R(2,0),线段GR的垂直平分线交直线GF于H.
上任意一点,R(2,0),线段GR的垂直平分线交直线GF于H.
(1)求点H的轨迹C的方程;
(2)点M(1,0),P、Q是轨迹C上的两点,直线PQ过圆心F(―2,0),且F在线段PQ之间,求△PQM面积的最小值.
答案
解:(1)点H的轨迹C的方程为![]()
(2)设![]()
若![]()
![]()
若PQ不垂直于x轴,设直线![]()
∵F在P、Q两点之间,∴P、Q在双曲线的左支上,且![]()
又双曲线的渐近线为: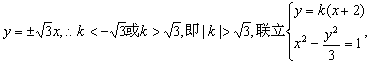
消去x,整理得![]()
![]()
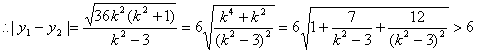
![]()
综上可知:△PQM面积的最小值是9.

