如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-LB是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系。
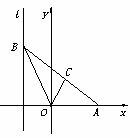
答案
解法一:依题意,记B(-1,b) (b∈R),则直线OA和OB的方程分别y=0和y=-bx.设点C(x,y),则有
0≤x<a,由OC平分∠AOB,知点C到OA、OB距离相等根据点到直线的距离公式得|y|= ![]() ①
①
依题设,点C在直线AB上,故有:y=![]()
由x-a≠0,得b=![]() ②
②
将②式代入①式得:
y2[1+![]() ]=[y-
]=[y-![]() ]2
]2
整理得:y2[(1-a)x2-2ax+(1+a)y2]=0
若y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a);
若y=0,则b=0,∠AOB=π,点C的坐标为(0,0)满足上式
综上得点C的轨迹方程为:(1-a)x2-2ax+(1+a)y2=0(0≤x<a)
∵ a≠1,
∴ ③
③
由此知,当0<a<1时,方程③表示椭圆弧段;当a>1时,方程③表示双曲线一支的弧段
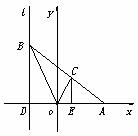
解法二:如图,设D是l与x轴的交点,过点C作CE⊥x轴,E是垂足
(Ⅰ)当|BD|≠0时,设点C(x,y),则0<x<a,y≠0
由CE∥BD,得![]()
∵∠COA=∠COB=∠COD-∠BOD=π-∠COA-∠BOD
∴2∠COA=π-∠BOD
∵tg(2∠COA)=![]() ,
,
tg(π-∠BOD)=-tg∠BOD,
![]()
![]()
∴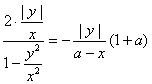
整理得:(1-a)x2-2ax+(1+a)y2=0(0<x<a)
(Ⅱ)当|BD|=0时,∠BOA=π,则点C的坐标为(0,0),满足上式
综合(Ⅰ)(Ⅱ),得点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a)
以下同解法一.
