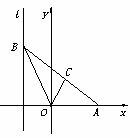设椭圆![]() 的两个焦点是
的两个焦点是![]() 与
与![]() ,且椭圆上存在点P,使得直线PF2与直线PF2垂直.
,且椭圆上存在点P,使得直线PF2与直线PF2垂直.
(1)求实数m的取值范围;
(2)设L是相应于焦点F2的准线,直线PF2与L相交于点Q. 若![]() ,求直线PF2的方程.
,求直线PF2的方程.
答案
解:(1)由题设有![]()
设点P的坐标为(![]() ),由
),由![]() ,得
,得![]() ,
,
化简得 ![]() ①
①
将①与![]() 联立,解得
联立,解得 ![]()
由![]()
所以m的取值范围是![]() .
.
(2)准线L的方程为![]() 设点Q的坐标为
设点Q的坐标为![]() ,则
,则![]()
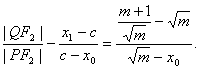 ②
②
将![]() 代入②,化简得
代入②,化简得![]()
由题设![]() ,得
,得 ![]() ,无解.
,无解.
将![]() 代入②,化简得
代入②,化简得
![]()
由题设![]() ,得
,得 ![]()
解得m=2.
从而![]() 得到PF2的方程
得到PF2的方程
![]()