答案
思路点拨：本题是有关排列组合的常见问题，可以考虑直接法与间接法（排除法），注意考虑分步去确定，并且注意全面地考虑问题.
解法一：（间接法）：由数字0，1，2，3，4，5所组成的没有重复数字的四位数有
×
=300个，其中能被5整除的数即个位为0或5的数共有
+
·
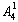=60+48=108个（其中A35表示个位是0的四位数的个数，
×
表示个位是5的四位数的个数），所以满足题目的约束条件的四位数共有300-108=192个.
解法一：（直接法）：由于所求的四位数不能被5整除，所以其个位不能是0与5，因此个位上的数可以从1，2，3，4这四个数字中任选一个，有
种选法，接着从剩余的四个数字（除0外）中任选一个作为千位上的数字，有
种选法，最后从剩余的四个数字中任选两个作为百位、十位上的数字，有
种选法，所以由分步计数乘法原理知，满足题目的约束条件的四位数共有
×
×
=192个.
答案：192
[一通百通]对于此类排列组合问题，其中含有特殊元素与特殊位置，在处理过程中尤其要注意全面地考虑问题，否则就会出错.对于特殊元素的处理，可以首先满足特殊要求或采用排除法将问题解决.
